The Scientist and Engineer's Guide to
Digital Signal Processing
By Steven W. Smith, Ph.D.
Book Search
Table of contents
- 1: The Breadth and Depth of DSP
- 2: Statistics, Probability and Noise
- 3: ADC and DAC
- 4: DSP Software
- 5: Linear Systems
- 6: Convolution
- 7: Properties of Convolution
- 8: The Discrete Fourier Transform
- 9: Applications of the DFT
- 10: Fourier Transform Properties
- 11: Fourier Transform Pairs
- 12: The Fast Fourier Transform
- 13: Continuous Signal Processing
- 14: Introduction to Digital Filters
- 15: Moving Average Filters
- 16: Windowed-Sinc Filters
- 17: Custom Filters
- 18: FFT Convolution
- 19: Recursive Filters
- 20: Chebyshev Filters
- 21: Filter Comparison
- 22: Audio Processing
- 23: Image Formation & Display
- 24: Linear Image Processing
- 25: Special Imaging Techniques
- 26: Neural Networks (and more!)
- 27: Data Compression
- 28: Digital Signal Processors
- 29: Getting Started with DSPs
- 30: Complex Numbers
- 31: The Complex Fourier Transform
- 32: The Laplace Transform
- 33: The z-Transform
- 34: Explaining Benford's Law
How to order your own hardcover copy
Wouldn't you rather have a bound book instead of 640 loose pages?Your laser printer will thank you!
Order from Amazon.com.
Chapter 27: Data Compression
This method is named after D.A. Huffman, who developed the procedure in the 1950s. Figure 27-2 shows a histogram of the byte values from a large ASCII file. More than 96% of this file consists of only 31 characters: the lower case letters, the space, the comma, the period, and the carriage return. This observation can be used to make an appropriate compression scheme for this file. To start, we will assign each of these 31 common characters a five bit binary code: 00000 = "a", 00001 = "b", 00010 = "c", etc. This allows 96% of the file to be reduced in size by 5/8. The last of the five bit codes, 11111, will be a flag indicating that the character being transmitted is not one of the 31 common characters. The next eight bits in the file indicate what the character is, according to the standard ASCII assignment. This results in 4% of the characters in the input file requiring 5+8=13 bits. The idea is to assign frequently used characters fewer bits,
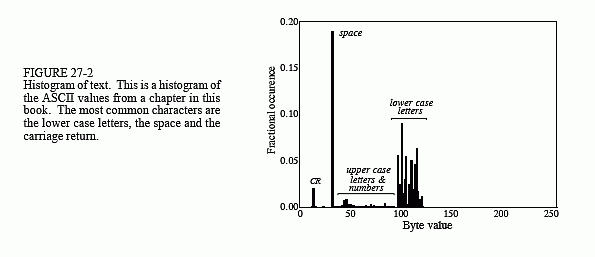
and seldom used characters more bits. In this example, the average number of bits required per original character is: 0.96×5 + 0.04×13 = 5.32. In other words, an overall compression ratio of: 8 bits/5.32 bits, or about 1.5:1.
Huffman encoding takes this idea to the extreme. Characters that occur most often, such the space and period, may be assigned as few as one or two bits. Infrequently used characters, such as: !, @, #, $ and %, may require a dozen or more bits. In mathematical terms, the optimal situation is reached when the number of bits used for each character is proportional to the logarithm of the character's probability of occurrence.
A clever feature of Huffman encoding is how the variable length codes can be packed together. Imagine receiving a serial data stream of ones and zeros. If each character is represented by eight bits, you can directly separate one character from the next by breaking off 8 bit chunks. Now consider a Huffman encoded data stream, where each character can have a variable number of bits. How do you separate one character from the next? The answer lies in the proper selection of the Huffman codes that enable the correct separation. An example will illustrate how this works.
Figure 27-3 shows a simplified Huffman encoding scheme. The characters A through G occur in the original data stream with the probabilities shown. Since the character A is the most common, we will represent it with a single bit, the code: 1. The next most common character, B, receives two bits, the code: 01. This continues to the least frequent character, G, being assigned six bits, 000011. As shown in this illustration, the variable length codes are resorted into eight bit groups, the standard for computer use.
When uncompression occurs, all the eight bit groups are placed end-to-end to form a long serial string of ones and zeros. Look closely at the encoding table of Fig. 27-3, and notice how each code consists of two parts: a number of zeros before a one, and an optional binary code after the one. This allows the binary data stream to be separated into codes without the need for delimiters or other marker between the codes. The uncompression program
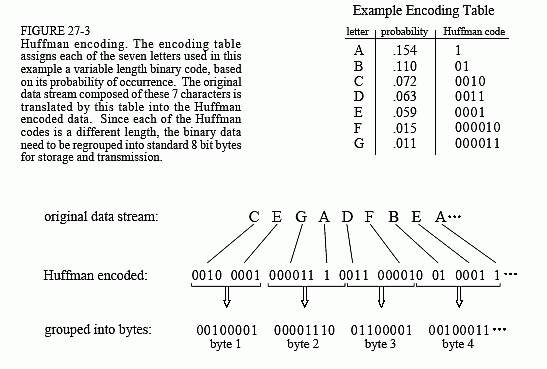
looks at the stream of ones and zeros until a valid code is formed, and then starting over looking for the next character. The way that the codes are formed insures that no ambiguity exists in the separation.
A more sophisticated version of the Huffman approach is called arithmetic encoding. In this scheme, sequences of characters are represented by individual codes, according to their probability of occurrence. This has the advantage of better data compression, say 5-10%. Run-length encoding followed by either Huffman or arithmetic encoding is also a common strategy. As you might expect, these types of algorithms are very complicated, and usually left to data compression specialists.
To implement Huffman or arithmetic encoding, the compression and un-compression algorithms must agree on the binary codes used to represent each character (or groups of characters). This can be handled in one of two
ways. The simplest is to use a predefined encoding table that is always the same, regardless of the information being compressed. More complex schemes use encoding optimized for the particular data being used. This requires that the encoding table be included in the compressed file for use by the uncompression program. Both methods are common.
