The Scientist and Engineer's Guide to
Digital Signal Processing
By Steven W. Smith, Ph.D.
Book Search
Table of contents
- 1: The Breadth and Depth of DSP
- 2: Statistics, Probability and Noise
- 3: ADC and DAC
- 4: DSP Software
- 5: Linear Systems
- 6: Convolution
- 7: Properties of Convolution
- 8: The Discrete Fourier Transform
- 9: Applications of the DFT
- 10: Fourier Transform Properties
- 11: Fourier Transform Pairs
- 12: The Fast Fourier Transform
- 13: Continuous Signal Processing
- 14: Introduction to Digital Filters
- 15: Moving Average Filters
- 16: Windowed-Sinc Filters
- 17: Custom Filters
- 18: FFT Convolution
- 19: Recursive Filters
- 20: Chebyshev Filters
- 21: Filter Comparison
- 22: Audio Processing
- 23: Image Formation & Display
- 24: Linear Image Processing
- 25: Special Imaging Techniques
- 26: Neural Networks (and more!)
- 27: Data Compression
- 28: Digital Signal Processors
- 29: Getting Started with DSPs
- 30: Complex Numbers
- 31: The Complex Fourier Transform
- 32: The Laplace Transform
- 33: The z-Transform
- 34: Explaining Benford's Law
How to order your own hardcover copy
Wouldn't you rather have a bound book instead of 640 loose pages?Your laser printer will thank you!
Order from Amazon.com.
Chapter 25: Special Imaging Techniques
Suppose we want to compare two imaging systems, with the goal of determining which has the best spatial resolution. In other words, we want to know which system can detect the smallest object. To simplify things, we would like the answer to be a single number for each system. This allows a direct comparison upon which to base design decisions. Unfortunately, a single parameter is not always sufficient to characterize all the subtle aspects of imaging. This is complicated by the fact that spatial resolution is limited by two distinct but interrelated effects: sample spacing and sampling aperture size. This section contains two main topics: (1) how a single parameter can best be used to characterize spatial resolution, and (2) the relationship between sample spacing and sampling aperture size.
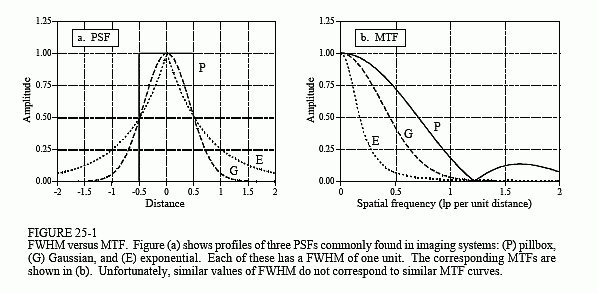
Figure 25-1a shows profiles from three circularly symmetric PSFs: the pillbox, the Gaussian, and the exponential. These are representative of the PSFs commonly found in imaging systems. As described in the last chapter, the pillbox can result from an improperly focused lens system. Likewise, the Gaussian is formed when random errors are combined, such as viewing stars through a turbulent atmosphere. An exponential PSF is generated when electrons or x-rays strike a phosphor layer and are converted into
light. This is used in radiation detectors, night vision light amplifiers, and CRT displays. The exact shape of these three PSFs is not important for this discussion, only that they broadly represent the PSFs seen in real world applications.
The PSF contains complete information about the spatial resolution. To express the spatial resolution by a single number, we can ignore the shape of the PSF and simply measure its width. The most common way to specify this is by the Full-Width-at-Half-Maximum (FWHM) value. For example, all the PSFs in (a) have an FWHM of 1 unit.
Unfortunately, this method has two significant drawbacks. First, it does not match other measures of spatial resolution, including the subjective judgement of observers viewing the images. Second, it is usually very difficult to directly measure the PSF. Imagine feeding an impulse into an imaging system; that is, taking an image of a very small white dot on a black background. By definition, the acquired image will be the PSF of the system. The problem is, the measured PSF will only contain a few pixels, and its contrast will be low. Unless you are very careful, random noise will swamp the measurement. For instance, imagine that the impulse image is a 512×512 array of all zeros except for a single pixel having a value of 255. Now compare this to a normal image where all of the 512×512 pixels have an average value of about 128. In loose terms, the signal in the impulse image is about 100,000 times weaker than a normal image. No wonder the signal-to-noise ratio will be bad; there's hardly any signal!
A basic theme throughout this book is that signals should be understood in the domain where the information is encoded. For instance, audio signals should be dealt with in the frequency domain, while image signals should be handled in the spatial domain. In spite of this, one way to measure image resolution is by looking at the frequency response. This goes against the fundamental philosophy of this book; however, it is a common method and you need to become familiar with it.
Taking the two-dimensional Fourier transform of the PSF provides the two-dimensional frequency response. If the PSF is circularly symmetric, its frequency response will also be circularly symmetric. In this case, complete information about the frequency response is contained in its profile. That is, after calculating the frequency domain via the FFT method, columns 0 to N/2 in row 0 are all that is needed. In imaging jargon, this display of the frequency response is called the Modulation Transfer Function (MTF). Figure 25-1b shows the MTFs for the three PSFs in (a). In cases where the PSF is not circularly symmetric, the entire two-dimensional frequency response contains information. However, it is usually sufficient to know the MTF curves in the vertical and horizontal directions (i.e., columns 0 to N/2 in row 0, and rows 0 to N/2 in column 0). Take note: this procedure of extracting a row or column from the two-dimensional frequency spectrum is not equivalent to taking the one-dimensional FFT of the profiles shown in (a). We will come back to this issue shortly. As shown in Fig. 25-1, similar values of FWHM do not correspond to similar MTF curves.
Figure 25-2 shows a line pair gauge, a device used to measure image resolution via the MTF. Line pair gauges come in different forms depending on the particular application. For example, the black and white pattern shown in this figure could be directly used to test video cameras. For an x-ray imaging system, the ribs might be made from lead, with an x-ray transparent material between. The key feature is that the black and white lines have a closer spacing toward one end. When an image is taken of a line pair gauge, the lines at the closely spaced end will be blurred together, while at the other end they will be distinct. Somewhere in the middle the lines will be just barely separable. An observer looks at the image, identifies this location, and reads the corresponding resolution on the calibrated scale.
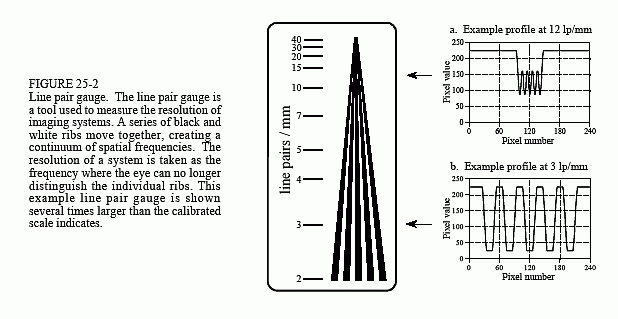
The way that the ribs blur together is important in understanding the limitations of this measurement. Imagine acquiring an image of the line pair gauge in Fig. 25-2. Figures (a) and (b) show examples of the profiles at low and high spatial frequencies. At the low frequency, shown in (b), the curve is flat on the top and bottom, but the edges are blurred, At the higher spatial frequency, (a), the amplitude of the modulation has been reduced. This is exactly what the MTF curve in Fig. 25-1b describes: higher spatial frequencies are reduced in amplitude. The individual ribs will be distinguishable in the image as long as the amplitude is greater than about 3% to 10% of the original height. This is related to the eye's ability to distinguish the low contrast difference between the peaks and valleys in the presence of image noise.
A strong advantage of the line pair gauge measurement is that it is simple and fast. The strongest disadvantage is that it relies on the human eye, and therefore has a certain subjective component. Even if the entire MTF curve is measured, the most common way to express the system resolution is to quote the frequency where the MTF is reduced to either 3%, 5% or 10%. Unfortunately, you will not always be told which of these values is being used; product data sheets frequently use vague terms such as "limiting resolution." Since manufacturers like their specifications to be as good as possible (regardless of what the device actually does), be safe and interpret these ambiguous terms to mean 3% on the MTF curve.
A subtle point to notice is that the MTF is defined in terms of sine waves, while the line pair gauge uses square waves. That is, the ribs are uniformly dark regions separated by uniformly light regions. This is done for manufacturing convenience; it is very difficult to make lines that have a sinusoidally varying darkness. What are the consequences of using a square wave to measure the MTF? At high spatial frequencies, all frequency components but the fundamental of the square wave have been removed. This causes the modulation to appear sinusoidal, such as is shown in Fig. 25-2a. At low frequencies, such as shown in Fig. 25-2b, the wave appears square. The fundamental sine wave contained in a square wave has an amplitude of 4/π = 1.27 times the amplitude of the square wave (see Table 13-10). The result: the line pair gauge provides a slight overestimate of the true resolution of the system, by starting with an effective amplitude of more than pure black to pure white. Interesting, but almost always ignored.
Since square waves and sine waves are used interchangeably to measure the MTF, a special terminology has arisen. Instead of the word "cycle," those in imaging use the term line pair (a dark line next to a light line). For example, a spatial frequency would be referred to as 25 line pairs per millimeter, instead of 25 cycles per millimeter.
The width of the PSF doesn't track well with human perception and is difficult to measure. The MTF methods are in the wrong domain for understanding how resolution affects the encoded information. Is there a more favorable alternative? The answer is yes, the line spread function (LSF) and the edge response. As shown in Fig. 25-3, the line spread
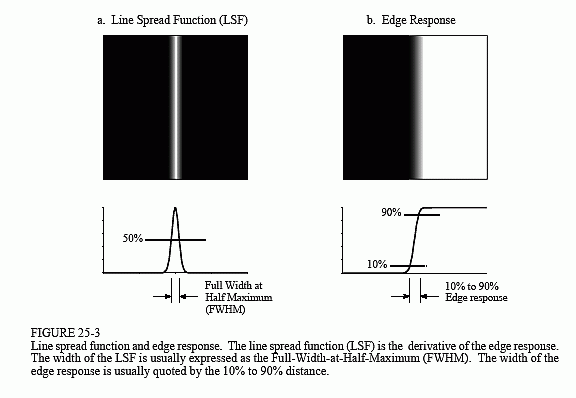
function is the response of the system to a thin line across the image. Similarly, the edge response is how the system responds to a sharp straight discontinuity (an edge). Since a line is the derivative (or first difference) of an edge, the LSF is the derivative (or first difference) of the edge response. The single parameter measurement used here is the distance required for the edge response to rise from 10% to 90%.
There are many advantages to using the edge response for measuring resolution. First, the measurement is in the same form as the image information is encoded. In fact, the main reason for wanting to know the resolution of a system is to understand how the edges in an image are blurred. The second advantage is that the edge response is simple to measure because edges are easy to generate in images. If needed, the LSF can easily be found by taking the first difference of the edge response.
The third advantage is that all common edges responses have a similar shape, even though they may originate from drastically different PSFs. This is shown in Fig. 25-4a, where the edge responses of the pillbox, Gaussian, and exponential PSFs are displayed. Since the shapes are similar, the 10%-90% distance is an excellent single parameter measure of resolution. The fourth advantage is that the MTF can be directly found by taking the one-dimensional FFT of the LSF (unlike the PSF to MTF calculation that must use a two-dimensional Fourier transform). Figure 25-4b shows the MTFs corresponding to the edge responses of (a). In other words, the curves in (a) are converted into the curves in (b) by taking the first difference (to find the LSF), and then taking the FFT.
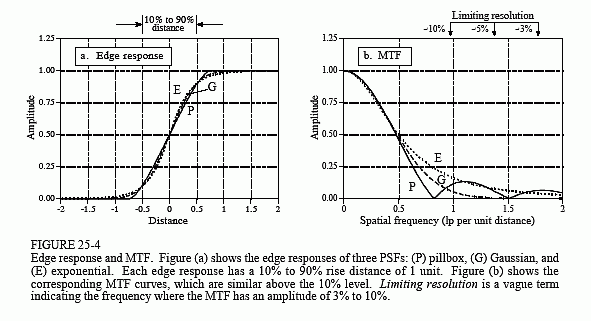
The fifth advantage is that similar edge responses have similar MTF curves, as shown in Figs. 25-4 (a) and (b). This allows us to easily convert between the two measurements. In particular, a system that has a 10%-90% edge response of x distance, has a limiting resolution (10% contrast) of about 1 line pair per x distance. The units of the "distance" will depend on the type of system being dealt with. For example, consider three different imaging systems that have 10%-90% edge responses of 0.05 mm, 0.2 milliradian and 3.3 pixels. The 10% contrast level on the corresponding MTF curves will occur at about: 20 lp/mm, 5 lp/milliradian and 0.33 lp/pixel, respectively.
Figure 25-5 illustrates the mathematical relationship between the PSF and the LSF. Figure (a) shows a pillbox PSF, a circular area of value 1, displayed as white, surrounded by a region of all zeros, displayed as gray. A profile of the PSF (i.e., the pixel values along a line drawn across the center of the image) will be a rectangular pulse. Figure (b) shows the corresponding LSF. As shown, the LSF is mathematically equal to the integrated profile of the PSF. This is found by sweeping across the image in some direction, as illustrated by the rays (arrows). Each value in the integrated profile is the sum of the pixel values along the corresponding ray.
In this example where the rays are vertical, each point in the integrated profile is found by adding all the pixel values in each column. This corresponds to the LSF of a line that is vertical in the image. The LSF of a line that is horizontal in the image is found by summing all of the pixel values in each row. For continuous images these concepts are the same, but the summations are replaced by integrals.
As shown in this example, the LSF can be directly calculated from the PSF. However, the PSF cannot always be calculated from the LSF. This is because the PSF contains information about the spatial resolution in all directions, while the LSF is limited to only one specific direction. A system

has only one PSF, but an infinite number of LSFs, one for each angle. For example, imagine a system that has an oblong PSF. This makes the spatial resolution different in the vertical and horizontal directions, resulting in the LSF being different in these directions. Measuring the LSF at a single angle does not provide enough information to calculate the complete PSF except in the special instance where the PSF is circularly symmetric. Multiple LSF measurements at various angles make it possible to calculate a non-circular PSF; however, the mathematics is quite involved and usually not worth the effort. In fact, the problem of calculating the PSF from a number of LSF measurements is exactly the same problem faced in computed tomography, discussed later in this chapter.
As a practical matter, the LSF and the PSF are not dramatically different for most imaging systems, and it is very common to see one used as an approximation for the other. This is even more justifiable considering that there are two common cases where they are identical: the rectangular PSF has a rectangular LSF (with the same widths), and the Gaussian PSF has a Gaussian LSF (with the same standard deviations).
These concepts can be summarized into two skills: how to evaluate a resolution specification presented to you, and how to measure a resolution specification of your own. Suppose you come across an advertisement stating: "This system will resolve 40 line pairs per millimeter." You should interpret this to mean: "A sinusoid of 40 lp/mm will have its amplitude reduced to 3%-10% of its true value, and will be just barely visible in the image." You should also do the mental calculation that 40 lp/mm @ 10% contrast is equal to a 10%-90% edge response of 1/(40 lp/mm) = 0.025 mm. If the MTF specification is for a 3% contrast level, the edge response will be about 1.5 to 2 times wider.
When you measure the spatial resolution of an imaging system, the steps are carried out in reverse. Place a sharp edge in the image, and measure the resulting edge response. The 10%-90% distance of this curve is the best single parameter measurement of the system's resolution. To keep your boss and the marketing people happy, take the first difference of the edge response to find the LSF, and then use the FFT to find the MTF.
