The Scientist and Engineer's Guide to
Digital Signal Processing
By Steven W. Smith, Ph.D.
Book Search
Table of contents
- 1: The Breadth and Depth of DSP
- 2: Statistics, Probability and Noise
- 3: ADC and DAC
- 4: DSP Software
- 5: Linear Systems
- 6: Convolution
- 7: Properties of Convolution
- 8: The Discrete Fourier Transform
- 9: Applications of the DFT
- 10: Fourier Transform Properties
- 11: Fourier Transform Pairs
- 12: The Fast Fourier Transform
- 13: Continuous Signal Processing
- 14: Introduction to Digital Filters
- 15: Moving Average Filters
- 16: Windowed-Sinc Filters
- 17: Custom Filters
- 18: FFT Convolution
- 19: Recursive Filters
- 20: Chebyshev Filters
- 21: Filter Comparison
- 22: Audio Processing
- 23: Image Formation & Display
- 24: Linear Image Processing
- 25: Special Imaging Techniques
- 26: Neural Networks (and more!)
- 27: Data Compression
- 28: Digital Signal Processors
- 29: Getting Started with DSPs
- 30: Complex Numbers
- 31: The Complex Fourier Transform
- 32: The Laplace Transform
- 33: The z-Transform
- 34: Explaining Benford's Law
How to order your own hardcover copy
Wouldn't you rather have a bound book instead of 640 loose pages?Your laser printer will thank you!
Order from Amazon.com.
Chapter 7: Properties of Convolution
Delta Function
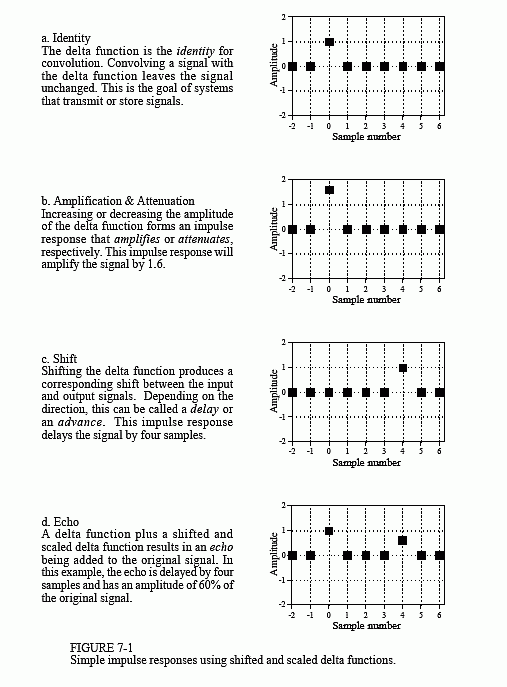
The simplest impulse response is nothing more that a delta function, as shown
in Fig. 7-1a. That is, an impulse on the input produces an identical impulse on
the output. This means that all signals are passed through the system without
change. Convolving any signal with a delta function results in exactly the same
signal. Mathematically, this is written:
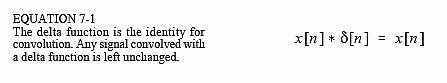
This property makes the delta function the identity for convolution. This is analogous to zero being the identity for addition (a + 0 = a), and one being the identity for multiplication (a×1 = a). At first glance, this type of system may seem trivial and uninteresting. Not so! Such systems are the ideal for data storage, communication and measurement. Much of DSP is concerned with passing information through systems without change or degradation.
Figure 7-1b shows a slight modification to the delta function impulse response. If the delta function is made larger or smaller in amplitude, the resulting system is an amplifier or attenuator, respectively. In equation form, amplification results if k is greater than one, and attenuation results if k is less than one:
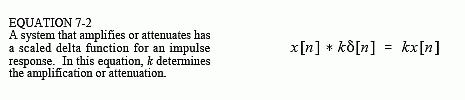
The impulse response in Fig. 7-1c is a delta function with a shift. This results in a system that introduces an identical shift between the input and output signals. This could be described as a signal delay, or a signal advance, depending on the direction of the shift. Letting the shift be represented by the parameter, s, this can be written as the equation:
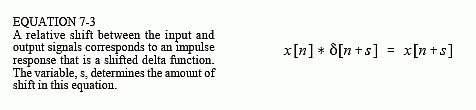
Science and engineering are filled with cases where one signal is a shifted version of another. For example, consider a radio signal transmitted from a remote space probe, and the corresponding signal received on the earth. The time it takes the radio wave to propagate over the distance causes a delay between the two signals. In biology, the electrical signals in adjacent nerve cells are shifted versions of each other, as determined by the time it takes an action potential to cross the synaptic junction that connects the two.
Figure 7-1d shows an impulse response composed of a delta function plus a shifted and scaled delta function. By superposition, the output of this system is the input signal plus a delayed version of the input signal, i.e., an echo. Echoes are important in many DSP applications. The addition of echoes is a key part in making audio recordings sound natural and pleasant. Radar and sonar analyze echoes to detect aircraft and submarines. Geophysicists use echoes to find oil. Echoes are also very important in telephone networks, because you want to avoid them.
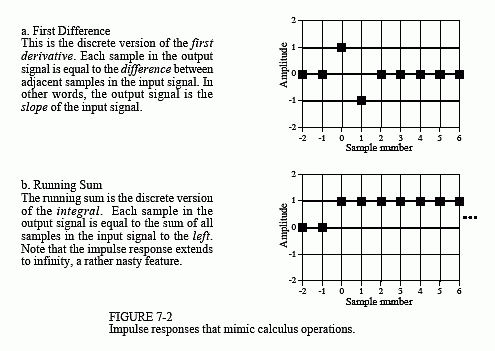
Calculus-like Operations
Convolution can change discrete signals in ways that resemble integration and
differentiation. Since the terms "derivative" and "integral" specifically refer to
operations on continuous signals, other names are given to their discrete
counterparts. The discrete operation that mimics the first derivative is called the
first difference. Likewise, the discrete form of the integral is called the
running sum. It is also common to hear these operations called the discrete
derivative and the discrete integral, although mathematicians frown when they hear these informal terms used.
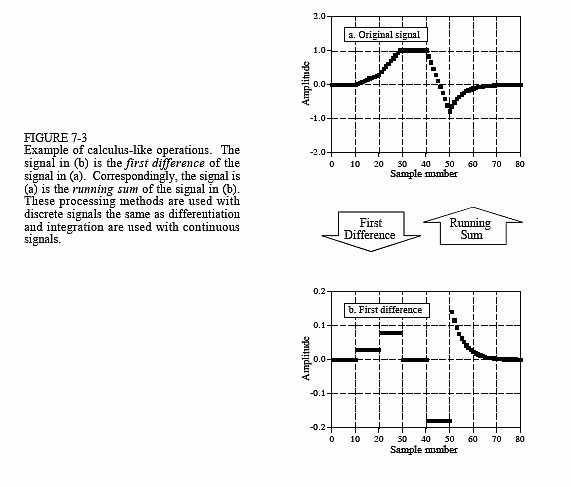
Figure 7-2 shows the impulse responses that implement the first difference and the running sum. Figure 7-3 shows an example using these operations. In 7-3a, the original signal is composed of several sections with varying slopes. Convolving this signal with the first difference impulse response produces the signal in Fig. 7-3b. Just as with the first derivative, the amplitude of each point in the first difference signal is equal to the slope at the corresponding location in the original signal. The running sum is the inverse operation of the first difference. That is, convolving the signal in (b), with the running sum's impulse response, produces the signal in (a).
These impulse responses are simple enough that a full convolution program is usually not needed to implement them. Rather, think of them in the alternative mode: each sample in the output signal is a sum of weighted samples from the input. For instance, the first difference can be calculated:

That is, each sample in the output signal is equal to the difference between two adjacent samples in the input signal. For instance, y[40] = x[40] - x[39]. It should be mentioned that this is not the only way to define a discrete derivative. Another common method is to define the slope symmetrically around the point being examined, such as: y[n] = (x[n+1] - x[n-1])/2.
Using this same approach, each sample in the running sum can be calculated by summing all points in the original signal to the left of the sample's location. For instance, if y[n] is the running sum of x[n], then sample y[40] is found by adding samples x[0] through x[40]. Likewise, sample y[41] is found by adding samples x[0] through x[41]. Of course, it would be very inefficient to calculate the running sum in this manner. For example, if y[40] has already been calculated, y[41] can be calculated with only a single addition: y[41] = x[41] + y[40]. In equation form:
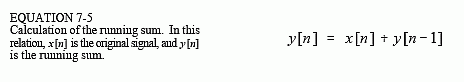
Relations of this type are called recursion equations or difference equations. We will revisit them in Chapter 19. For now, the important idea to understand is that these relations are identical to convolution using the impulse responses of Fig. 7-2. Table 7-1 provides computer programs that implement these calculus-like operations.

Low-pass and High-pass Filters
The design of digital filters is covered in detail in later chapters. For now, be
satisfied to understand the general shape of low-pass and high-pass filter kernels
(another name for a filter's impulse response). Figure 7-4 shows several
common low-pass filter kernels. In general, low-pass filter kernels are
composed of a group of adjacent positive points. This results in each sample in
the output signal being a weighted average of many adjacent points from the
input signal. This averaging smoothes the signal, thereby removing high-frequency components. As shown by the sinc function in (c), some low-pass
filter kernels include a few negative valued samples in the tails. Just as in
analog electronics, digital low-pass filters are used for noise reduction, signal
separation, wave shaping, etc.
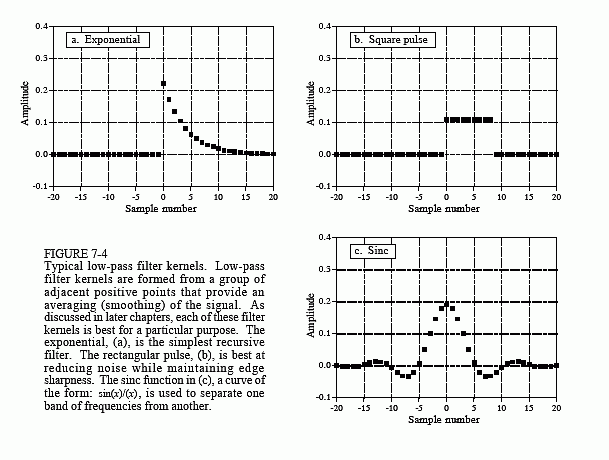
The cutoff frequency of the filter is changed by making filter kernel wider or narrower. If a low-pass filter has a gain of one at DC (zero frequency), then the sum of all of the points in the impulse response must be equal to one. As illustrated in (a) and (c), some filter kernels theoretically extend to infinity without dropping to a value of zero. In actual practice, the tails are truncated after a certain number of samples, allowing it to be represented by a finite number of points. How else could it be stored in a computer?
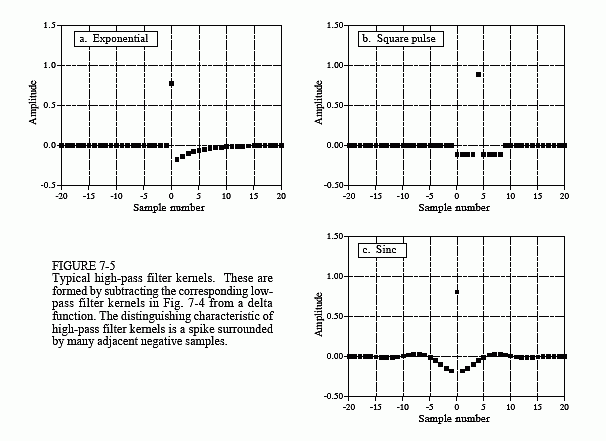
Figure 7-5 shows three common high-pass filter kernels, derived from the corresponding low-pass filter kernels in Fig. 7-4. This is a common strategy in filter design: first devise a low-pass filter and then transform it to what you need, high-pass, band-pass, band-reject, etc. To understand the low-pass to high-pass transform, remember that a delta function impulse response passes the entire signal, while a low-pass impulse response passes only the low-frequency components. By superposition, a filter kernel consisting of a delta function minus the low-pass filter kernel will pass the entire signal minus the low-frequency components. A high-pass filter is born! As shown in Fig. 7-5, the delta function is usually added at the center of symmetry, or sample zero if the filter kernel is not symmetrical. High-pass filters have zero gain at DC (zero frequency), achieved by making the sum of all the points in the filter kernel equal to zero.
Causal and Noncausal Signals
Imagine a simple analog electronic circuit. If you apply a short pulse to the
input, you will see a response on the output. This is the kind of cause and effect
that our universe is based on. One thing we definitely know: any effect must
happen after the cause. This is a basic characteristic of what we call time. Now
compare this to a DSP system that changes an input signal into an output signal,
both stored in arrays in a computer. If this mimics a real world system, it must
follow the same principle of causality as the real world does. For example, the
value at sample number eight in the input signal can only affect sample number
eight or greater in the output signal. Systems that operate in this manner are
said to be causal. Of course, digital processing doesn't necessarily have to
function this way. Since both the input and output signals are arrays of numbers
stored in a computer, any of the input signal values can affect any of the output
signal values.
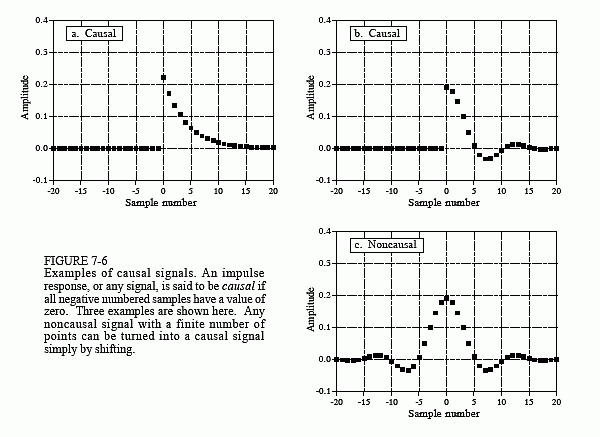
As shown by the examples in Fig. 7-6, the impulse response of a causal system must have a value of zero for all negative numbered samples. Think of this from the input side view of convolution. To be causal, an impulse in the input signal at sample number n must only affect those points in the output signal with a sample number of n or greater. In common usage, the term causal is applied to any signal where all the negative numbered samples have a value of zero, whether it is an impulse response or not.
Zero Phase, Linear Phase, and Nonlinear Phase
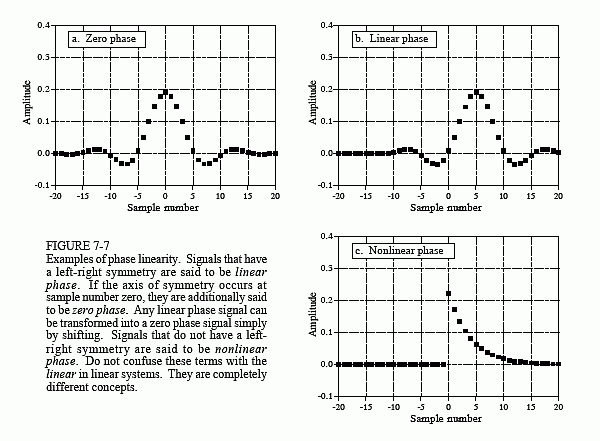
As shown in Fig. 7-7, a signal is said to be zero phase if it has left-right
symmetry around sample number zero. A signal is said to be linear phase if it
has left-right symmetry, but around some point other than zero. This means that
any linear phase signal can be changed into a zero phase signal simply by
shifting left or right. Lastly, a signal is said to be nonlinear phase if it does not
have left-right symmetry.
You are probably thinking that these names don't seem to follow from their definitions. What does phase have to do with symmetry? The answer lies in the frequency spectrum, and will be discussed in more detail in later chapters. Briefly, the frequency spectrum of any signal is composed of two parts, the magnitude and the phase. The frequency spectrum of a signal that is symmetrical around zero has a phase that is zero. Likewise, the frequency spectrum of a signal that is symmetrical around some nonzero point has a phase that is a straight line, i.e., a linear phase. Lastly, the frequency spectrum of a signal that is not symmetrical has a phase that is not a straight line, i.e., it has a nonlinear phase.
A special note about the potentially confusing terms: linear and nonlinear phase. What does this have to do the concept of system linearity discussed in previous chapters? Absolutely nothing! System linearity is the broad concept that nearly all of DSP is based on (superposition, homogeneity, additivity, etc). Linear and nonlinear phase mean that the phase is, or is not, a straight line. In fact, a system must be linear even to say that the phase is zero, linear, or nonlinear.
