The Scientist and Engineer's Guide to
Digital Signal Processing
By Steven W. Smith, Ph.D.
Book Search
Table of contents
- 1: The Breadth and Depth of DSP
- 2: Statistics, Probability and Noise
- 3: ADC and DAC
- 4: DSP Software
- 5: Linear Systems
- 6: Convolution
- 7: Properties of Convolution
- 8: The Discrete Fourier Transform
- 9: Applications of the DFT
- 10: Fourier Transform Properties
- 11: Fourier Transform Pairs
- 12: The Fast Fourier Transform
- 13: Continuous Signal Processing
- 14: Introduction to Digital Filters
- 15: Moving Average Filters
- 16: Windowed-Sinc Filters
- 17: Custom Filters
- 18: FFT Convolution
- 19: Recursive Filters
- 20: Chebyshev Filters
- 21: Filter Comparison
- 22: Audio Processing
- 23: Image Formation & Display
- 24: Linear Image Processing
- 25: Special Imaging Techniques
- 26: Neural Networks (and more!)
- 27: Data Compression
- 28: Digital Signal Processors
- 29: Getting Started with DSPs
- 30: Complex Numbers
- 31: The Complex Fourier Transform
- 32: The Laplace Transform
- 33: The z-Transform
- 34: Explaining Benford's Law
How to order your own hardcover copy
Wouldn't you rather have a bound book instead of 640 loose pages?Your laser printer will thank you!
Order from Amazon.com.
Chapter 13: Continuous Signal Processing
Just as with discrete signals, the convolution of continuous signals can be viewed from the input signal, or the output signal. The input side viewpoint is the best conceptual description of how convolution operates. In comparison, the output side viewpoint describes the mathematics that must be used. These descriptions are virtually identical to those presented in Chapter 6 for discrete signals.
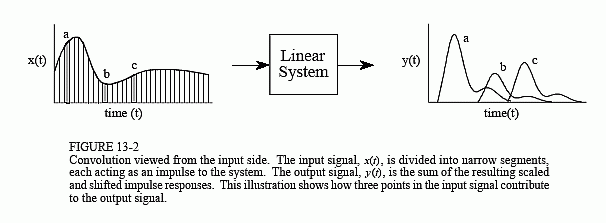
Figure 13-2 shows how convolution is viewed from the input side. An input signal, x(t), is passed through a system characterized by an impulse response, h(t), to produce an output signal, y(t). This can be written in the familiar mathematical equation, y(t) = x(t) * h(t). The input signal is divided into narrow columns, each short enough to act as an impulse to the system. In other words, the input signal is decomposed into an infinite number of scaled and shifted delta functions. Each of these impulses produces a scaled and shifted version of the impulse response in the output signal. The final output signal is then equal to the combined effect, i.e., the sum of all of the individual responses.
For this scheme to work, the width of the columns must be much shorter than the response of the system. Of course, mathematicians take this to the extreme by making the input segments infinitesimally narrow, turning the situation into a calculus problem. In this manner, the input viewpoint describes how a single point (or narrow region) in the input signal affects a larger portion of output signal.
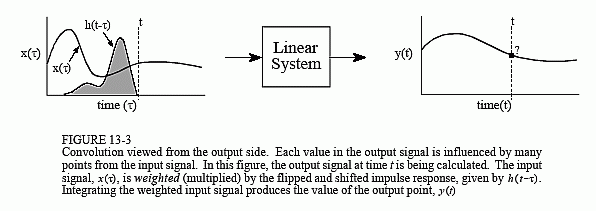
In comparison, the output viewpoint examines how a single point in the output signal is determined by the various values from the input signal. Just as with discrete signals, each instantaneous value in the output signal is affected by a section of the input signal, weighted by the impulse response flipped left-for-right. In the discrete case, the signals are multiplied and summed. In the continuous case, the signals are multiplied and integrated. In equation form:
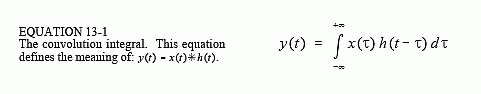
This equation is called the convolution integral, and is the twin of the convolution sum (Eq. 6-1) used with discrete signals. Figure 13-3 shows how this equation can be understood. The goal is to find an expression for calculating the value of the output signal at an arbitrary time, t. The first step is to change the independent variable used to move through the input signal and the impulse response. That is, we replace t with τ (a lower case
Greek tau). This makes x(t) and h(t) become x(τ) and h(τ), respectively. This change of variable names is needed because t is already being used to represent the point in the output signal being calculated. The next step is to flip the impulse response left-for-right, turning it into h(-τ). Shifting the flipped impulse response to the location t, results in the expression becoming h(t-τ). The input signal is then weighted by the flipped and shifted impulse response by multiplying the two, i.e., x(τ)h(t-τ). The value of the output signal is then found by integrating this weighted input signal from negative to positive infinity, as described by Eq. 13-1.
If you have trouble understanding how this works, go back and review the same concepts for discrete signals in Chapter 6. Figure 13-3 is just another way of describing the convolution machine in Fig. 6-8. The only difference is that integrals are being used instead of summations. Treat this as an extension of what you already know, not something new.
An example will illustrate how continuous convolution is used in real world problems and the mathematics required. Figure 13-4 shows a simple continuous linear system: an electronic low-pass filter composed of a single resistor and a single capacitor. As shown in the figure, an impulse entering this system produces an output that quickly jumps to some value, and then exponentially decays toward zero. In other words, the impulse response of this simple electronic circuit is a one-sided exponential. Mathematically, the
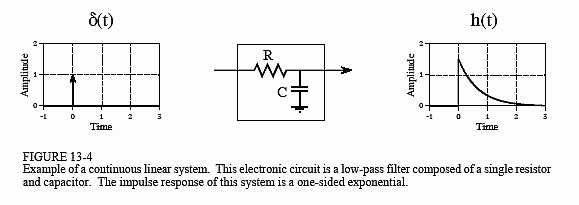
impulse response of this system is broken into two sections, each represented by an equation:
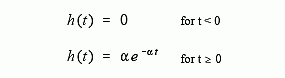
where α = 1/RC (R is in ohms, C is in farads, and t is in seconds). Just as in the discrete case, the continuous impulse response contains complete information about the system, that is, how it will react to all possible signals. To pursue this example further, Fig. 13-5 shows a square pulse entering the system, mathematically expressed by:
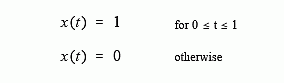
Since both the input signal and the impulse response are completely known as mathematical expressions, the output signal, y(t), can be calculated by evaluating the convolution integral of Eq. 13-1. This is complicated by the fact that both signals are defined by regions rather than a single
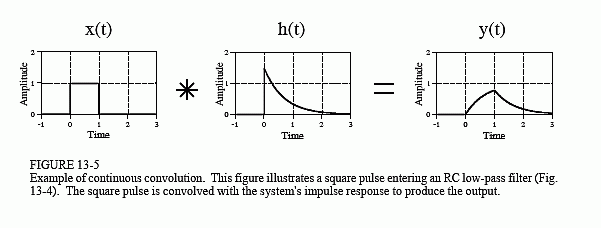
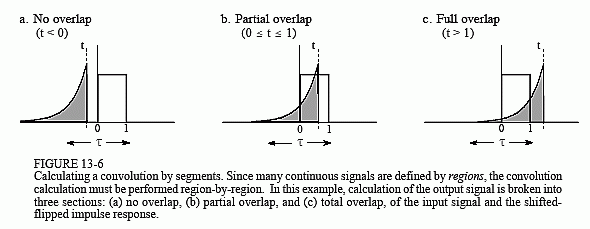
mathematical expression. This is very common in continuous signal processing. It is usually essential to draw a picture of how the two signals shift over each other for various values of t. In this example, Fig. 13-6a shows that the two signals do not overlap at all for . This means that the product of the two signals is zero at all locations along the τ axis, and the resulting output signal is:

A second case is illustrated in (b), where t is between 0 and 1. Here the two signals partially overlap, resulting in their product having nonzero values between τ = 0 and &tau = t. Since this is the only nonzero region, it is the only section where the integral needs to be evaluated. This provides the output signal for 0 ≤ t ≤ 1, given by:
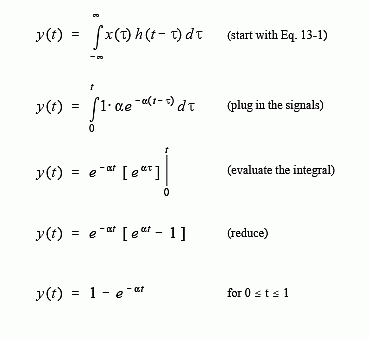
Figure (c) shows the calculation for the third section of the output signal, where t > 1. Here the overlap occurs between τ = 0 and τ = 1, making the calculation the same as for the second segment, except a change to the limits of integration:
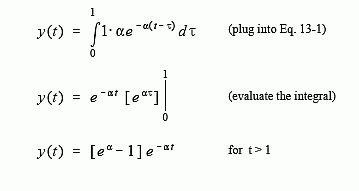
The waveform in each of these three segments should agree with your knowledge of electronics: (1) The output signal must be zero until the input signal becomes nonzero. That is, the first segment is given by y(t) = 0 for t < 0. (2) When the step occurs, the RC circuit exponentially increases to match the input, according to the equation: y(t) = 1 - e-αt. (3) When the input is returned to zero, the output exponentially decays toward zero, given by the equation: y(t) = ke-αt (where k = eα - 1, the voltage on the capacitor just before the discharge was started).
More intricate waveforms can be handled in the same way, although the mathematical complexity can rapidly become unmanageable. When faced with a nasty continuous convolution problem, you need to spend significant time evaluating strategies for solving the problem. If you start blindly evaluating integrals you are likely to end up with a mathematical mess. A common strategy is to break one of the signals into simpler additive components that can be individually convolved. Using the principles of linearity, the resulting waveforms can be added to find the answer to the original problem.
Figure 13-7 shows another strategy: modify one of the signals in some linear way, perform the convolution, and then undo the original modification. In this example the modification is the derivative, and it is undone by taking the integral. The derivative of a unit amplitude square pulse is two impulses, the first with an area of one, and the second with an area of negative one. To understand this, think about the opposite process of taking the integral of the two impulses. As you integrate past the first impulse, the integral rapidly increases from zero to one, i.e., a step function. After passing the negative impulse, the integral of the signal rapidly returns from one back to zero, completing the square pulse.
Taking the derivative simplifies this problem because convolution is easy when one of the signals is composed of impulses. Each of the two impulses in x'(t) contributes a scaled and shifted version of the impulse response to
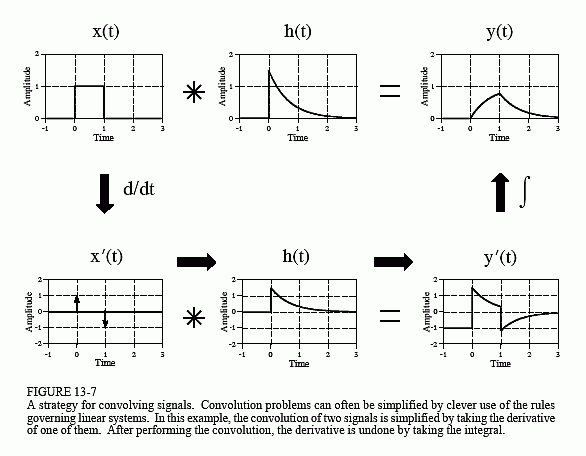
the derivative of the output signal, y'(t). That is, by inspection it is known that: y'(t) = h(t) - h(t - 1) . The output signal, y(t), can then be found by plugging in the exact equation for h(t), and integrating the expression.
A slight nuisance in this procedure is that the DC value of the input signal is lost when the derivative is taken. This can result in an error in the DC value of the calculated output signal. The mathematics reflects this as the arbitrary constant that can be added during the integration. There is no systematic way of identifying this error, but it can usually be corrected by inspection of the problem. For instance, there is no DC error in the example of Fig. 13-7. This is known because the calculated output signal has the correct DC value when t becomes very large. If an error is present in a particular problem, an appropriate DC term is manually added to the output signal to complete the calculation.
This method also works for signals that can be reduced to impulses by taking the derivative multiple times. In the jargon of the field, these signals are called piecewise polynomials. After the convolution, the initial operation of multiple derivatives is undone by taking multiple integrals. The only catch is that the lost DC value must be found at each stage by finding the correct constant of integration.
Before starting a difficult continuous convolution problem, there is another approach that you should consider. Ask yourself the question: Is a mathematical expression really needed for the output signal, or is a graph of the waveform sufficient? If a graph is adequate, you may be better off to handle the problem with discrete techniques. That is, approximate the continuous signals by samples that can be directly convolved by a computer program. While not as mathematically pure, it can be much easier.
