The Scientist and Engineer's Guide to
Digital Signal Processing
By Steven W. Smith, Ph.D.
Book Search
Table of contents
- 1: The Breadth and Depth of DSP
- 2: Statistics, Probability and Noise
- 3: ADC and DAC
- 4: DSP Software
- 5: Linear Systems
- 6: Convolution
- 7: Properties of Convolution
- 8: The Discrete Fourier Transform
- 9: Applications of the DFT
- 10: Fourier Transform Properties
- 11: Fourier Transform Pairs
- 12: The Fast Fourier Transform
- 13: Continuous Signal Processing
- 14: Introduction to Digital Filters
- 15: Moving Average Filters
- 16: Windowed-Sinc Filters
- 17: Custom Filters
- 18: FFT Convolution
- 19: Recursive Filters
- 20: Chebyshev Filters
- 21: Filter Comparison
- 22: Audio Processing
- 23: Image Formation & Display
- 24: Linear Image Processing
- 25: Special Imaging Techniques
- 26: Neural Networks (and more!)
- 27: Data Compression
- 28: Digital Signal Processors
- 29: Getting Started with DSPs
- 30: Complex Numbers
- 31: The Complex Fourier Transform
- 32: The Laplace Transform
- 33: The z-Transform
- 34: Explaining Benford's Law
How to order your own hardcover copy
Wouldn't you rather have a bound book instead of 640 loose pages?Your laser printer will thank you!
Order from Amazon.com.
Chapter 29: Getting Started with DSPs
In this last example, we took advantage of one of the SHARC DSP's key features, its ability to handle floating point calculations. Even though the samples are in a fixed point format when passed to and from the codec, we go to the trouble of converting them to floating point for the intermediate FIR filtering algorithm. As discussed in the last chapter, there are two reasons for wanting to process the data with floating point math: ease of programming, and performance. Does it really make a difference?
For the programmer, yes, it makes a large difference. Floating point code is far easier to write. Look back at the assembly program in Table 29-2. There are only two lines (41 and 42) in the main FIR filter. In contrast, the fixed point programmer must add code to manage the data at each math calculation. To avoid overflow and underflow, the values must be checked for size and, if needed, scaled accordingly. The intermediate results will also need to be stored in an extended precision accumulator to avoid the devastating effects of repeated round-off error.
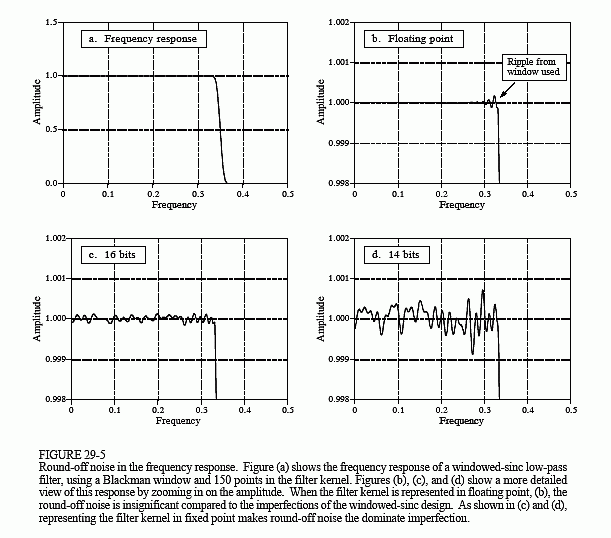
The issue of performance is much more subtle. For example, Fig. 29-5a shows an FIR low-pass filter with a moderately sharp cutoff, as described in Chapter 16. This "large scale" curve would look the same whether fixed or floating point were used in the calculation. To see the difference between these two methods, we must zoom in on the amplitude by a factor of several hundred as shown in (b), (c), and (d). Here we can see a clear difference. The floating point execution, (b), has such low round-off noise that its performance is limited by the way we designed the filter kernel. The 0.02% overshoot near the transition is a characteristic of the Blackman window used in this filter. The point is, if we want to improve the performance, we need to work on the algorithm, not the implementation. The curves in (c) and (d) show the round-off noise introduced when each point in the filter kernel is represented by 16 and 14 bits, respectively. A better algorithm would do nothing to make these better curves; the shape of the actual frequency response is swamped by noise.
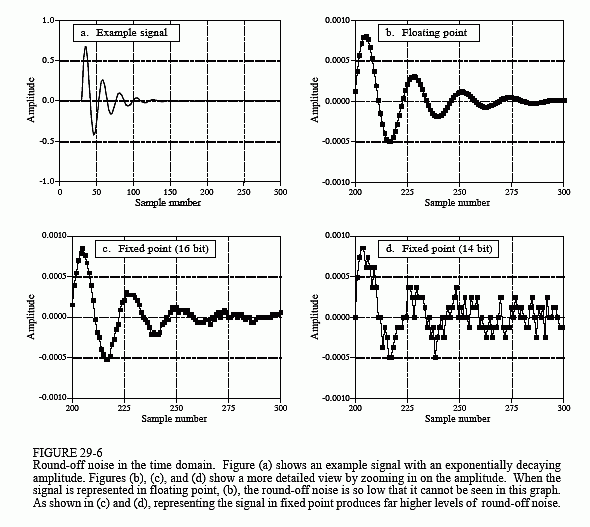
Figure 29-6 shows the difference between fixed and floating point in the time domain. Figure (a) shows a wiggly signal that exponentially decreases in amplitude. This might represent, for example, the sound wave from a plucked string, or the shaking of the ground from a distant explosion. As before, this "large scale" waveform would look the same whether fixed or floating point were used to represent the samples. To see the difference,
we must zoom in on the amplitude, as shown in (b), (c) and (d). As discussed in Chapter 3, this quantization appears much as additive random noise, limiting the detectability of small components in the signals.
These performance differences between fixed and floating point are often not important; for instance, they cannot even be seen in the "large scale" signals of Fig. 29-5a and Fig. 29-6a. However, there are some applications where the extra performance of floating point is helpful, and may even be critical. For instance, high-fidelity consumer audio system, such as CD players, represent the signals with 16 bit fixed point. In most cases, this exceeds the capability of human hearing. However, the best professional audio systems sample the signals with as high as 20 to 24 bits, leaving absolutely no room for artifacts that might contaminate the music. Floating point is nearly ideal for algorithms that process these high-precision digital signals.
Another case where the higher performance of floating point is needed is when the algorithm is especially sensitive to noise. For instance, FIR
filters are quite insensitive to round-off effects. As shown in Fig. 29-5, round-off noise doesn't change the overall shape of the frequency response; the entire curve just becomes noisier. IIR filters are a different story; round-off can cause all sorts of havoc, including making them unstable. Floating point allows these algorithms to achieve better performance in cutoff frequency sharpness, stopband attenuation, and step response overshoot.
