The Scientist and Engineer's Guide to
Digital Signal Processing
By Steven W. Smith, Ph.D.
Book Search
Table of contents
- 1: The Breadth and Depth of DSP
- 2: Statistics, Probability and Noise
- 3: ADC and DAC
- 4: DSP Software
- 5: Linear Systems
- 6: Convolution
- 7: Properties of Convolution
- 8: The Discrete Fourier Transform
- 9: Applications of the DFT
- 10: Fourier Transform Properties
- 11: Fourier Transform Pairs
- 12: The Fast Fourier Transform
- 13: Continuous Signal Processing
- 14: Introduction to Digital Filters
- 15: Moving Average Filters
- 16: Windowed-Sinc Filters
- 17: Custom Filters
- 18: FFT Convolution
- 19: Recursive Filters
- 20: Chebyshev Filters
- 21: Filter Comparison
- 22: Audio Processing
- 23: Image Formation & Display
- 24: Linear Image Processing
- 25: Special Imaging Techniques
- 26: Neural Networks (and more!)
- 27: Data Compression
- 28: Digital Signal Processors
- 29: Getting Started with DSPs
- 30: Complex Numbers
- 31: The Complex Fourier Transform
- 32: The Laplace Transform
- 33: The z-Transform
- 34: Explaining Benford's Law
How to order your own hardcover copy
Wouldn't you rather have a bound book instead of 640 loose pages?Your laser printer will thank you!
Order from Amazon.com.
Chapter 20: Chebyshev Filters
The Chebyshev response is a mathematical strategy for achieving a faster roll-off by allowing ripple in the frequency response. Analog and digital filters that use this approach are called Chebyshev filters. For instance, analog Chebyshev filters were used in Chapter 3 for analog-to-digital and digital-to-analog conversion. These filters are named from their use of the Chebyshev polynomials, developed by the Russian mathematician Pafnuti Chebyshev (1821-1894). This name has been translated from Russian and appears in the literature with different spellings, such as: Chebychev, Tschebyscheff, Tchebysheff and Tchebichef.
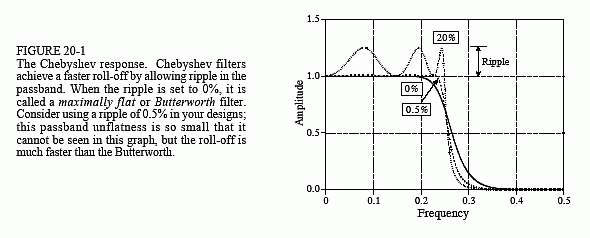
Figure 20-1 shows the frequency response of low-pass Chebyshev filters with passband ripples of: 0%, 0.5% and 20%. As the ripple increases (bad), the roll-off becomes sharper (good). The Chebyshev response is an optimal trade-off between these two parameters. When the ripple is set to 0%, the filter is called a maximally flat or Butterworth filter (after S. Butterworth, a British engineer who described this response in 1930). A ripple of 0.5% is a often good choice for digital filters. This matches the typical precision and accuracy of the analog electronics that the signal has passed through.
The Chebyshev filters discussed in this chapter are called type 1 filters, meaning that the ripple is only allowed in the passband. In comparison,
type 2 Chebyshev filters have ripple only in the stopband. Type 2 filters are seldom used, and we won't discuss them. There is, however, an important design called the elliptic filter, which has ripple in both the passband and the stopband. Elliptic filters provide the fastest roll-off for a given number of poles, but are much harder to design. We won't discuss the elliptic filter here, but be aware that it is frequently the first choice of professional filter designers, both in analog electronics and DSP. If you need this level of performance, buy a software package for designing digital filters.
