The Scientist and Engineer's Guide to
Digital Signal Processing
By Steven W. Smith, Ph.D.
Book Search
Table of contents
- 1: The Breadth and Depth of DSP
- 2: Statistics, Probability and Noise
- 3: ADC and DAC
- 4: DSP Software
- 5: Linear Systems
- 6: Convolution
- 7: Properties of Convolution
- 8: The Discrete Fourier Transform
- 9: Applications of the DFT
- 10: Fourier Transform Properties
- 11: Fourier Transform Pairs
- 12: The Fast Fourier Transform
- 13: Continuous Signal Processing
- 14: Introduction to Digital Filters
- 15: Moving Average Filters
- 16: Windowed-Sinc Filters
- 17: Custom Filters
- 18: FFT Convolution
- 19: Recursive Filters
- 20: Chebyshev Filters
- 21: Filter Comparison
- 22: Audio Processing
- 23: Image Formation & Display
- 24: Linear Image Processing
- 25: Special Imaging Techniques
- 26: Neural Networks (and more!)
- 27: Data Compression
- 28: Digital Signal Processors
- 29: Getting Started with DSPs
- 30: Complex Numbers
- 31: The Complex Fourier Transform
- 32: The Laplace Transform
- 33: The z-Transform
- 34: Explaining Benford's Law
How to order your own hardcover copy
Wouldn't you rather have a bound book instead of 640 loose pages?Your laser printer will thank you!
Order from Amazon.com.
Chapter 11: Fourier Transform Pairs
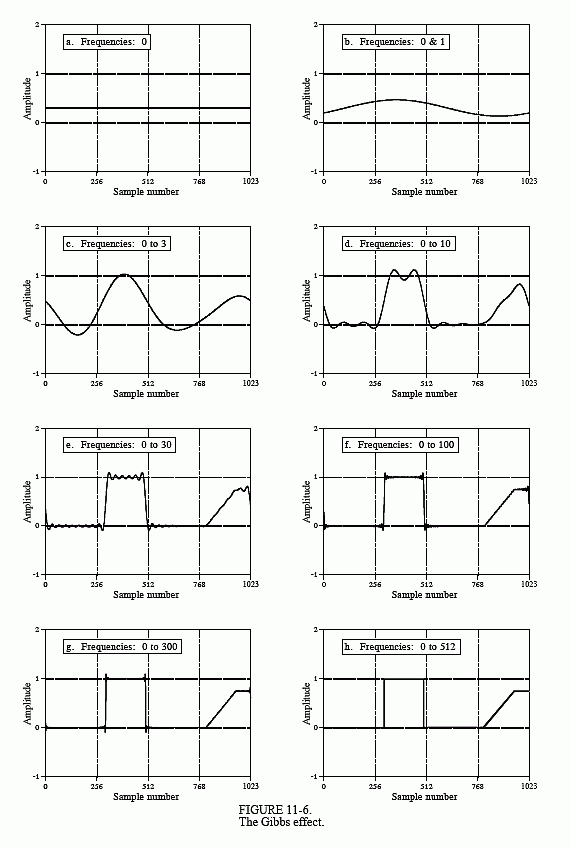
Figure 11-6 shows a time domain signal being synthesized from sinusoids. The signal being reconstructed is shown in the last graph, (h). Since this signal is 1024 points long, there will be 513 individual frequencies needed for a complete reconstruction. Figures (a) through (g) show what the reconstructed signal looks like if only some of these frequencies are used. For example, (f) shows a reconstructed signal using frequencies 0 through 100. This signal was created by taking the DFT of the signal in (h), setting frequencies 101 through 512 to a value of zero, and then using the Inverse DFT to find the resulting time domain signal.
As more frequencies are added to the reconstruction, the signal becomes closer to the final solution. The interesting thing is how the final solution is approached at the edges in the signal. There are three sharp edges in (h). Two are the edges of the rectangular pulse. The third is between sample numbers 1023 and 0, since the DFT views the time domain as periodic. When only some of the frequencies are used in the reconstruction, each edge shows overshoot and ringing (decaying oscillations). This overshoot and ringing is known as the Gibbs effect, after the mathematical physicist Josiah Gibbs, who explained the phenomenon in 1899.
Look closely at the overshoot in (e), (f), and (g). As more sinusoids are added, the width of the overshoot decreases; however, the amplitude of the overshoot remains about the same, roughly 9 percent. With discrete signals this is not a problem; the overshoot is eliminated when the last frequency is added. However, the reconstruction of continuous signals cannot be explained so easily. An infinite number of sinusoids must be added to synthesize a continuous signal. The problem is, the amplitude of the overshoot does not decrease as the number of sinusoids approaches infinity, it stays about the same 9%. Given this situation (and other arguments), it is reasonable to question if a summation of continuous sinusoids can reconstruct an edge. Remember the squabble between Lagrange and Fourier?
The critical factor in resolving this puzzle is that the width of the overshoot becomes smaller as more sinusoids are included. The overshoot is still present with an infinite number of sinusoids, but it has zero width. Exactly at the discontinuity the value of the reconstructed signal converges to the midpoint of the step. As shown by Gibbs, the summation converges to the signal in the sense that the error between the two has zero energy.
Problems related to the Gibbs effect are frequently encountered in DSP. For example, a low-pass filter is a truncation of the higher frequencies, resulting in overshoot and ringing at the edges in the time domain. Another common procedure is to truncate the ends of a time domain signal to prevent them from extending into neighboring periods. By duality, this distorts the edges in the frequency domain. These issues will resurface in future chapters on filter design.