The Scientist and Engineer's Guide to
Digital Signal Processing
By Steven W. Smith, Ph.D.
Book Search
Table of contents
- 1: The Breadth and Depth of DSP
- 2: Statistics, Probability and Noise
- 3: ADC and DAC
- 4: DSP Software
- 5: Linear Systems
- 6: Convolution
- 7: Properties of Convolution
- 8: The Discrete Fourier Transform
- 9: Applications of the DFT
- 10: Fourier Transform Properties
- 11: Fourier Transform Pairs
- 12: The Fast Fourier Transform
- 13: Continuous Signal Processing
- 14: Introduction to Digital Filters
- 15: Moving Average Filters
- 16: Windowed-Sinc Filters
- 17: Custom Filters
- 18: FFT Convolution
- 19: Recursive Filters
- 20: Chebyshev Filters
- 21: Filter Comparison
- 22: Audio Processing
- 23: Image Formation & Display
- 24: Linear Image Processing
- 25: Special Imaging Techniques
- 26: Neural Networks (and more!)
- 27: Data Compression
- 28: Digital Signal Processors
- 29: Getting Started with DSPs
- 30: Complex Numbers
- 31: The Complex Fourier Transform
- 32: The Laplace Transform
- 33: The z-Transform
- 34: Explaining Benford's Law
How to order your own hardcover copy
Wouldn't you rather have a bound book instead of 640 loose pages?Your laser printer will thank you!
Order from Amazon.com.
Chapter 21: Filter Comparison
Both the windowed-sinc and the Chebyshev filters are designed to separate one band of frequencies from another. The windowed-sinc is an FIR filter implemented by convolution, while the Chebyshev is an IIR filter carried out by recursion. Which is the best digital filter in the frequency domain? We'll let them fight it out.
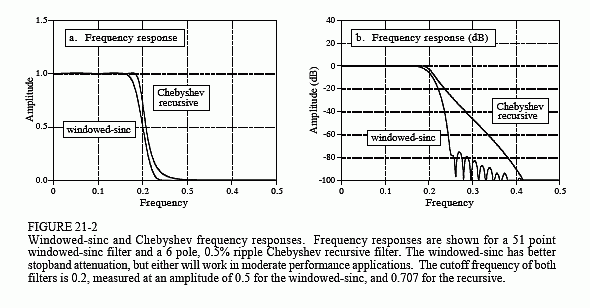
The recursive filter contender will be a 0.5% ripple, 6 pole Chebyshev low-pass filter. A fair comparison is complicated by the fact that the Chebyshev's frequency response changes with the cutoff frequency. We will use a cutoff frequency of 0.2, and select the windowed-sinc's filter kernel to be 51 points. This makes both filters have the same 90% to 10% roll-off, as shown in Fig. 21-2(a).
Now the pushing and shoving begins. The recursive filter has a 0.5% ripple in the passband, while the windowed-sinc is flat. However, we could easily set the recursive filter ripple to 0% if needed. No points. Figure 21-2b shows that the windowed-sinc has a much better stopband attenuation than the Chebyshev. One point for the windowed-sinc.
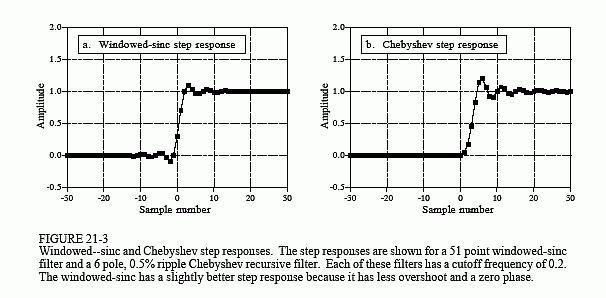
Figure 21-3 shows the step response of the two filters. Both are bad, as you should expect for frequency domain filters. The recursive filter has a nonlinear phase, but this can be corrected with bidirectional filtering. Since both filters are so ugly in this parameter, we will call this a draw.
So far, there isn't much difference between these two filters; either will work when moderate performance is needed. The heavy hitting comes over two critical issues: maximum performance and speed. The windowed-sinc is a powerhouse, while the Chebyshev is quick and agile. Suppose you have a really tough frequency separation problem, say, needing to isolate a 100
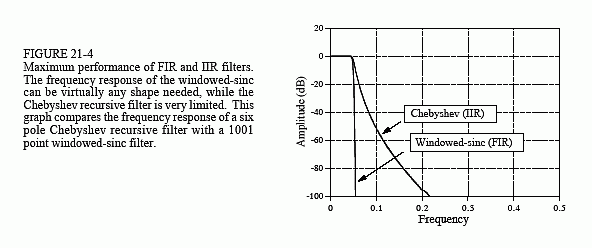
millivolt signal at 61 hertz that is riding on a 120 volt power line at 60 hertz. Figure 21-4 shows how these two filters compare when you need maximum performance. The recursive filter is a 6 pole Chebyshev with 0.5% ripple. This is the maximum number of poles that can be used at a 0.05 cutoff frequency with single precision. The windowed-sinc uses a 1001 point filter kernel, formed by convolving a 501 point windowed-sinc filter kernel with itself. As shown in Chapter 16, this provides greater stopband attenuation.
How do these two filters compare when maximum performance is needed? The windowed-sinc crushes the Chebyshev! Even if the recursive filter were improved (more poles, multistage implementation, double precision, etc.), it is still no match for the FIR performance. This is especially impressive when you consider that the windowed-sinc has only begun to fight. There are strong limits on the maximum performance that recursive filters can provide. The windowed-sinc, in contrast, can be pushed to incredible levels. This is, of course, provided you are willing to wait for the result. Which brings up the second critical issue: speed.
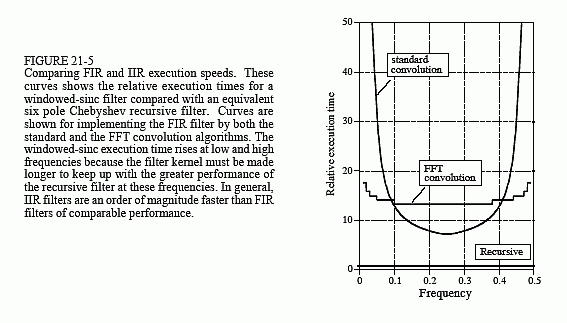
Comparing these filters for speed is like racing a Ferrari against a go-cart. Figure 21-5 shows how much longer the windowed-sinc takes to execute, compared to a six pole recursive filter. Since the recursive filter has a faster roll-off at low and high frequencies, the length of the windowed-sinc kernel must be made longer to match the performance (i.e., to keep the comparison fair). This accounts for the increased execution time for the windowed-sinc near frequencies 0 and 0.5. The important point is that FIR filters can be expected to be about an order of magnitude slower than comparable IIR filters (go-cart: 15 mph, Ferrari: 150 mph).
