The Scientist and Engineer's Guide to
Digital Signal Processing
By Steven W. Smith, Ph.D.
Book Search
Table of contents
- 1: The Breadth and Depth of DSP
- 2: Statistics, Probability and Noise
- 3: ADC and DAC
- 4: DSP Software
- 5: Linear Systems
- 6: Convolution
- 7: Properties of Convolution
- 8: The Discrete Fourier Transform
- 9: Applications of the DFT
- 10: Fourier Transform Properties
- 11: Fourier Transform Pairs
- 12: The Fast Fourier Transform
- 13: Continuous Signal Processing
- 14: Introduction to Digital Filters
- 15: Moving Average Filters
- 16: Windowed-Sinc Filters
- 17: Custom Filters
- 18: FFT Convolution
- 19: Recursive Filters
- 20: Chebyshev Filters
- 21: Filter Comparison
- 22: Audio Processing
- 23: Image Formation & Display
- 24: Linear Image Processing
- 25: Special Imaging Techniques
- 26: Neural Networks (and more!)
- 27: Data Compression
- 28: Digital Signal Processors
- 29: Getting Started with DSPs
- 30: Complex Numbers
- 31: The Complex Fourier Transform
- 32: The Laplace Transform
- 33: The z-Transform
- 34: Explaining Benford's Law
How to order your own hardcover copy
Wouldn't you rather have a bound book instead of 640 loose pages?Your laser printer will thank you!
Order from Amazon.com.
Chapter 34: Explaining Benford's Law
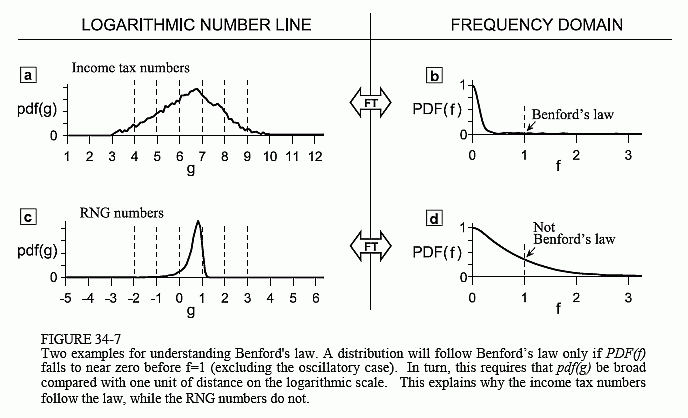
This last result is very surprising; the mystery of Benford's law turns out to be nothing more than distribution width. Figure 34-7 demonstrates this using our previous examples. Figures (a) and (c) are the histograms of the income tax return and the RNG numbers, respectively, on the logarithmic scale. Figure (b) and (d) are their Fourier Transforms. The Benford's Law Compliance Theorem tells us that (b) will follow Benford's law very closely, while (d) will follow it very poorly. That is, PDF(f) falls to near zero before f=1 for the income tax numbers, but does not for the RNG numbers. The next step of this is less rigorous, but still perfectly clear. Figure (b) falls to zero quickly because (a) is broad. Likewise, (d) falls to zero more slowly because (c) is narrow.
This also tells us something about the magic trick. If the distribution is wide compared with unit distance on the log axis, it means that the spread in the set of numbers being examined is much greater than ten. For instance, look back at the income tax numbers shown in Fig. 34-2a. The largest numbers in this set are about a million times greater in value than the smallest numbers. This extensive spread is a key part of stamping the logarithmic pattern into the data. That is, 543,923,100 must be divided by 100,000,000 to place it between 1 and 9.99999, while 1,221 only needs to be divided by 1,000. In other words, different numbers are being treated differently, all according to an anti-logarithmic pattern.
Now look at the RNG numbers in Fig. 34-2, a group that does not obey Benford's law. The largest numbers in this set are about four times the smallest numbers (measured from -σ to +σ). That is, they are grouped relatively close together in value. When we extract the leading digits from these numbers, most of them are treated exactly the same. For instance, both 7.844026 and 1.230605 are divided by 1 to place them between 1 and 9.999999. Likewise, numbers clustered around 5,000 would all be divided by 1,000 to extract the leading digits. Since the vast majority of the numbers are being treated the same, or nearly the same, the distortion of the data is relatively weak. That is, the logarithmic pattern cannot be introduced into the data, and the magic trick fails.
How does Benford's law behave in other bases? Suppose you repeat the previous derivation in base 4 instead of base 10. The base 4 logarithmic number line is used and the Benford's Law Compliance Theorem still holds. The difference comes in when we compare the width of our test distribution with one unit of distance on the logarithmic scale. One unit of distance in base 4 is only log10(4) = 0.602 the length of one unit in base 10, making it easier for the distribution to comply with Benford's law. In terms of the magic trick, the spread in the numbers being examined only needs to be much greater than four, rather than ten. In the common case where PDF(f) smoothly decreases, Benford's law will always be followed better when converted to a lower base, and worse if converted to a higher base. For instance, the income tax numbers will not follow Benford's law if converted to base 10,000 or above (making the unit distance on the log scale four times greater). Likewise, the RND number will follow Benford's law if converted to base 2 (shortening the unit distance to log10(2) = 0.301).
A note for advanced readers: You may have noticed a problem with this last statement, that is: all numbers in base 2 have a leading digit of 1. However, a more sophisticated definition of Benford's law can be used to eliminate issues of this sort. The leading digit of a number can be found by repeatedly multiplying/dividing the number by ten until it is between 1 and 9.99999, and then taking the integer portion. The advanced method stops after the first step, and directly looks at the pdf of the numbers running between 1 and 9.99999. We will call these the modified numbers. If Benford's law is being followed, a(n) = k/n, where a(n) is the probability density function of the modified numbers on the linear scale, and k is a constant providing unity area under the pdf curve. If needed for some purpose, we can find the fraction of numbers that have a leading digit of 1 by integrating a(n) from 1 to 2. Since the integral of k/n is the logarithm, if Benford's law is being followed this fraction is given by: log(2) - log(1) = 0.301. That is, we can easily move from the advanced representation to the simpler leading-digit definition.
This "k/n" form of Benford's law can be also derived from the method of Fig. 34-5. The fraction of the modified numbers that are greater than p but less than q is found by integrating a(n) between p and q. Further, this fraction will remain a constant under the scaling test if Benford's law is
being followed. However, this value is also equal to the average value of the appropriate scaling function. The logic here is the same used to show that the average value of ost(g) is equal to the average value of sf(g) in "Solving Mystery #1." These two factors become the left and right sides of the following equation, respectively:
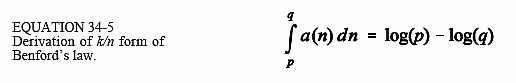
Solving this equation results in Benford's law, i.e., a(n) = k/n.
