The Scientist and Engineer's Guide to
Digital Signal Processing
By Steven W. Smith, Ph.D.
Book Search
Table of contents
- 1: The Breadth and Depth of DSP
- 2: Statistics, Probability and Noise
- 3: ADC and DAC
- 4: DSP Software
- 5: Linear Systems
- 6: Convolution
- 7: Properties of Convolution
- 8: The Discrete Fourier Transform
- 9: Applications of the DFT
- 10: Fourier Transform Properties
- 11: Fourier Transform Pairs
- 12: The Fast Fourier Transform
- 13: Continuous Signal Processing
- 14: Introduction to Digital Filters
- 15: Moving Average Filters
- 16: Windowed-Sinc Filters
- 17: Custom Filters
- 18: FFT Convolution
- 19: Recursive Filters
- 20: Chebyshev Filters
- 21: Filter Comparison
- 22: Audio Processing
- 23: Image Formation & Display
- 24: Linear Image Processing
- 25: Special Imaging Techniques
- 26: Neural Networks (and more!)
- 27: Data Compression
- 28: Digital Signal Processors
- 29: Getting Started with DSPs
- 30: Complex Numbers
- 31: The Complex Fourier Transform
- 32: The Laplace Transform
- 33: The z-Transform
- 34: Explaining Benford's Law
How to order your own hardcover copy
Wouldn't you rather have a bound book instead of 640 loose pages?Your laser printer will thank you!
Order from Amazon.com.
Chapter 21: Filter Comparison
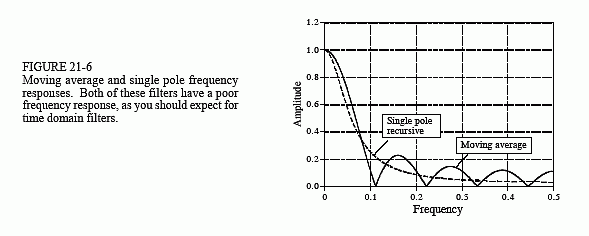
Our third competition will be a battle of the time domain filters. The first fighter will be a nine point moving average filter. Its opponent for today's match will be a single pole recursive filter using the bidirectional technique. To achieve a comparable frequency response, the single pole filter will use a sample-to-sample decay of x = 0.70. The battle begins in Fig. 21-6 where the frequency response of each filter is shown. Neither one is very impressive, but of course, frequency separation isn't what these filters are used for. No points for either side.
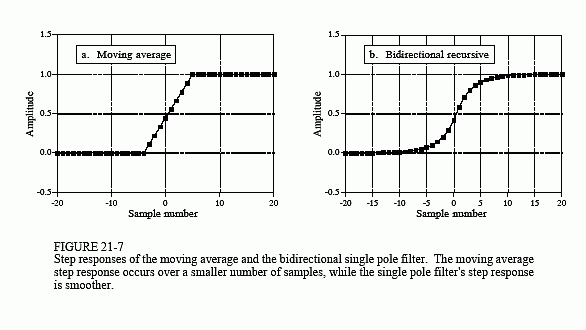
Figure 21-7 shows the step responses of the filters. In (a), the moving average step response is a straight line, the most rapid way of moving from one level to another. In (b), the recursive filter's step response is smoother, which may be better for some applications. One point for each side.
These filters are quite equally matched in terms of performance and often the choice between the two is made on personal preference. However,
there are two cases where one filter has a slight edge over the other. These are based on the trade-off between development time and execution time. In the first instance, you want to reduce development time and are willing to accept a slower filter. For example, you might have a one time need to filter a few thousand points. Since the entire program runs in only a few seconds, it is pointless to spend time optimizing the algorithm. Floating point will almost certainly be used. The choice is to use the moving average filter carried out by convolution, or a single pole recursive filter. The winner here is the recursive filter. It will be slightly easier to program and modify, and will execute much faster.
The second case is just the opposite; your filter must operate as fast as possible and you are willing to spend the extra development time to get it. For instance, this filter might be a part of a commercial product, with the potential to be run millions of times. You will probably use integers for the highest possible speed. Your choice of filters will be the moving average
carried out by recursion, or the single pole recursive filter implemented with look-up tables or integer math. The winner is the moving average filter. It will execute faster and not be susceptible to the development and execution problems of integer arithmetic.
