The Scientist and Engineer's Guide to
Digital Signal Processing
By Steven W. Smith, Ph.D.
Book Search
Table of contents
- 1: The Breadth and Depth of DSP
- 2: Statistics, Probability and Noise
- 3: ADC and DAC
- 4: DSP Software
- 5: Linear Systems
- 6: Convolution
- 7: Properties of Convolution
- 8: The Discrete Fourier Transform
- 9: Applications of the DFT
- 10: Fourier Transform Properties
- 11: Fourier Transform Pairs
- 12: The Fast Fourier Transform
- 13: Continuous Signal Processing
- 14: Introduction to Digital Filters
- 15: Moving Average Filters
- 16: Windowed-Sinc Filters
- 17: Custom Filters
- 18: FFT Convolution
- 19: Recursive Filters
- 20: Chebyshev Filters
- 21: Filter Comparison
- 22: Audio Processing
- 23: Image Formation & Display
- 24: Linear Image Processing
- 25: Special Imaging Techniques
- 26: Neural Networks (and more!)
- 27: Data Compression
- 28: Digital Signal Processors
- 29: Getting Started with DSPs
- 30: Complex Numbers
- 31: The Complex Fourier Transform
- 32: The Laplace Transform
- 33: The z-Transform
- 34: Explaining Benford's Law
How to order your own hardcover copy
Wouldn't you rather have a bound book instead of 640 loose pages?Your laser printer will thank you!
Order from Amazon.com.
Chapter 5: Linear Systems
A signal is a description of how one parameter varies with another parameter. For instance, voltage changing over time in an electronic circuit, or brightness varying with distance in an image. A system is any process that produces an output signal in response to an input signal. This is illustrated by the block diagram in Fig. 5-1. Continuous systems input and output continuous signals, such as in analog electronics. Discrete systems input and output discrete signals, such as computer programs that manipulate the values stored in arrays.
Several rules are used for naming signals. These aren't always followed in DSP, but they are very common and you should memorize them. The mathematics is difficult enough without a clear notation. First, continuous signals use parentheses, such as: x(t) and y(t), while discrete signals use brackets, as in: x[n] and y[n]. Second, signals use lower case letters. Upper case letters are reserved for the frequency domain, discussed in later chapters. Third, the name given to a signal is usually descriptive of the parameters it represents. For example, a voltage depending on time might be called: v(t), or a stock market price measured each day could be: p[d].
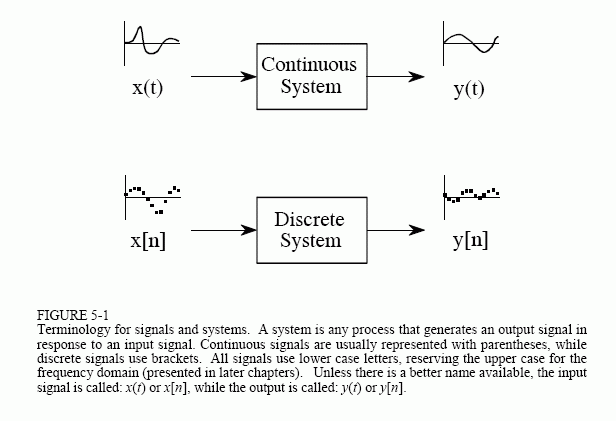
Signals and systems are frequently discussed without knowing the exact parameters being represented. This is the same as using x and y in algebra, without assigning a physical meaning to the variables. This brings in a fourth rule for naming signals. If a more descriptive name is not available, the input signal to a discrete system is usually called: x[n], and the output signal: y[n]. For continuous systems, the signals: x(t) and y(t) are used.
There are many reasons for wanting to understand a system. For example, you may want to design a system to remove noise in an electrocardiogram, sharpen an out-of-focus image, or remove echoes in an audio recording. In other cases, the system might have a distortion or interfering effect that you need to characterize or measure. For instance, when you speak into a telephone, you expect the other person to hear something that resembles your voice. Unfortunately, the input signal to a transmission line is seldom identical to the output signal. If you understand how the transmission line (the system) is changing the signal, maybe you can compensate for its effect. In still other cases, the system may represent some physical process that you want to study or analyze. Radar and sonar are good examples of this. These methods operate by comparing the transmitted and reflected signals to find the characteristics of a remote object. In terms of system theory, the problem is to find the system that changes the transmitted signal into the received signal.
At first glance, it may seem an overwhelming task to understand all of the possible systems in the world. Fortunately, most useful systems fall into a category called linear systems. This fact is extremely important. Without the linear system concept, we would be forced to examine the individual characteristics of many unrelated systems. With this approach, we can focus on the traits of the linear system category as a whole. Our first task is to identify what properties make a system linear, and how they fit into the everyday notion of electronics, software, and other signal processing systems.
