The Scientist and Engineer's Guide to
Digital Signal Processing
By Steven W. Smith, Ph.D.
Book Search
Table of contents
- 1: The Breadth and Depth of DSP
- 2: Statistics, Probability and Noise
- 3: ADC and DAC
- 4: DSP Software
- 5: Linear Systems
- 6: Convolution
- 7: Properties of Convolution
- 8: The Discrete Fourier Transform
- 9: Applications of the DFT
- 10: Fourier Transform Properties
- 11: Fourier Transform Pairs
- 12: The Fast Fourier Transform
- 13: Continuous Signal Processing
- 14: Introduction to Digital Filters
- 15: Moving Average Filters
- 16: Windowed-Sinc Filters
- 17: Custom Filters
- 18: FFT Convolution
- 19: Recursive Filters
- 20: Chebyshev Filters
- 21: Filter Comparison
- 22: Audio Processing
- 23: Image Formation & Display
- 24: Linear Image Processing
- 25: Special Imaging Techniques
- 26: Neural Networks (and more!)
- 27: Data Compression
- 28: Digital Signal Processors
- 29: Getting Started with DSPs
- 30: Complex Numbers
- 31: The Complex Fourier Transform
- 32: The Laplace Transform
- 33: The z-Transform
- 34: Explaining Benford's Law
How to order your own hardcover copy
Wouldn't you rather have a bound book instead of 640 loose pages?Your laser printer will thank you!
Order from Amazon.com.
Chapter 5: Linear Systems
A system is called linear if it has two mathematical properties: homogeneity (hōma-gen-ā-ity) and additivity. If you can show that a system has both properties, then you have proven that the system is linear. Likewise, if you can show that a system doesn't have one or both properties, you have proven that it isn't linear. A third property, shift invariance, is not a strict requirement for linearity, but it is a mandatory property for most DSP techniques. When you see the term linear system used in DSP, you should assume it includes shift invariance unless you have reason to believe otherwise. These three properties form the mathematics of how linear system theory is defined and used. Later in this chapter we will look at more intuitive ways of understanding linearity. For now, let's go through these formal mathematical properties.
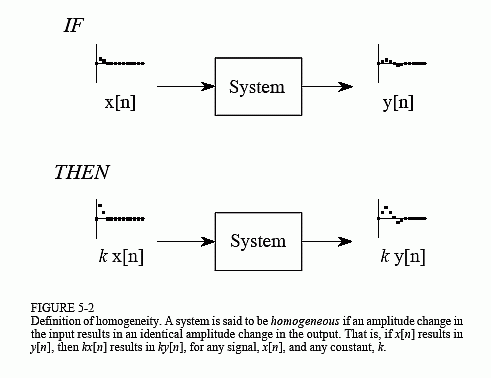
As illustrated in Fig. 5-2, homogeneity means that a change in the input signal's amplitude results in a corresponding change in the output signal's amplitude. In mathematical terms, if an input signal of x[n] results in an output signal of y[n], an input of kx[n] results in an output of ky[n], for any input signal and constant, k.
A simple resistor provides a good example of both homogenous and non-homogeneous systems. If the input to the system is the voltage across the resistor, v(t), and the output from the system is the current through the resistor, i(t) , the system is homogeneous. Ohm's law guarantees this; if the voltage is increased or decreased, there will be a corresponding increase or decrease in the current. Now, consider another system where the input signal is the voltage across the resistor, v(t), but the output signal is the power being dissipated in the resistor, p(t). Since power is proportional to the square of the voltage, if the input signal is increased by a factor of two, the output signal is increase by a factor of four. This system is not homogeneous and therefore cannot be linear.
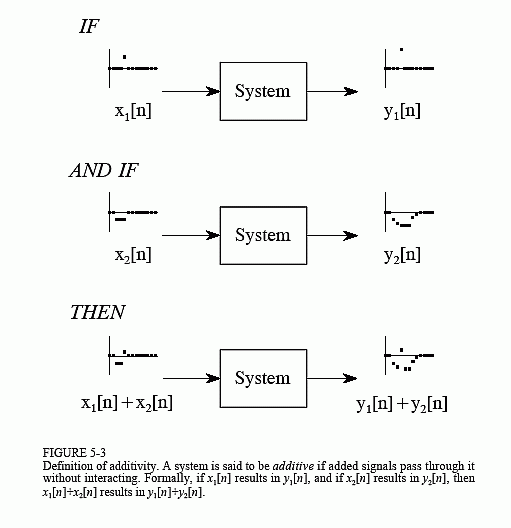
The property of additivity is illustrated in Fig. 5-3. Consider a system where an input of x1[n] produces an output of y1[n]. Further suppose that a different input, x2[n], produces another output, y2[n]. The system is said to be additive, if an input of x1[n] + x2[n] results in an output of y1[n] + y2[n], for all possible input signals. In words, signals added at the input produce signals that are added at the output.
The important point is that added signals pass through the system without interacting. As an example, think about a telephone conversation with your Aunt Edna and Uncle Bernie. Aunt Edna begins a rather lengthy story about how well her radishes are doing this year. In the background, Uncle Bernie is yelling at the dog for having an accident in his favorite chair. The two voice signals are added and electronically transmitted through the telephone network. Since this system is additive, the sound you hear is the sum of the two voices as they would sound if transmitted individually. You hear Edna and Bernie, not the creature, Ednabernie.
A good example of a nonadditive circuit is the mixer stage in a radio transmitter. Two signals are present: an audio signal that contains the voice or music, and a carrier wave that can propagate through space when applied to an antenna. The two signals are added and applied to a nonlinearity, such as a pn junction diode. This results in the signals merging to form a third signal, a modulated radio wave capable of carrying the information over great distances.
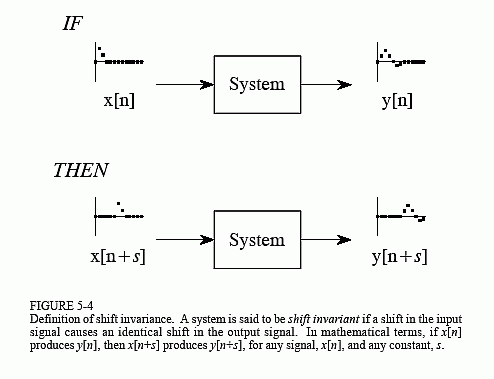
As shown in Fig. 5-4, shift invariance means that a shift in the input signal will result in nothing more than an identical shift in the output signal. In more formal terms, if an input signal of x[n] results in an output of y[n], an input signal of x[n + s] results in an output of y[n + s], for any input signal and any constant, s. Pay particular notice to how the mathematics of this shift is written, it will be used in upcoming chapters. By adding a constant, s, to the independent variable, n, the waveform can be advanced or retarded in the horizontal direction. For example, when s = 2, the signal is shifted left by two samples; when s = -2, the signal is shifted right by two samples.
Shift invariance is important because it means the characteristics of the system do not change with time (or whatever the independent variable happens to be). If a blip in the input causes a blop in the output, you can be assured that another blip will cause an identical blop. Most of the systems you encounter will be shift invariant. This is fortunate, because it is difficult to deal with systems that change their characteristics while in operation. For example, imagine that you have designed a digital filter to compensate for the degrading effects of a telephone transmission line. Your filter makes the voices sound more natural and easier to understand. Much to your surprise, along comes winter and you find the characteristics of the telephone line have changed with temperature. Your compensation filter is now mismatched and doesn't work especially well. This situation may require a more sophisticated algorithm that can adapt to changing conditions.
Why do homogeneity and additivity play a critical role in linearity, while shift invariance is something on the side? This is because linearity is a very broad concept, encompassing much more than just signals and systems. For example, consider a farmer selling oranges for $2 per crate and apples for $5 per crate. If the farmer sells only oranges, he will receive $20 for 10 crates, and $40 for 20 crates, making the exchange homogenous. If he sells 20 crates of oranges and 10 crates of apples, the farmer will receive: . This is the same amount as if the two had been sold individually, making the transaction additive. Being both homogenous and additive, this sale of goods is a linear process. However, since there are no signals involved, this is not a system, and shift invariance has no meaning. Shift invariance can be thought of as an additional aspect of linearity needed when signals and systems are involved.
