The Scientist and Engineer's Guide to
Digital Signal Processing
By Steven W. Smith, Ph.D.
Book Search
Table of contents
- 1: The Breadth and Depth of DSP
- 2: Statistics, Probability and Noise
- 3: ADC and DAC
- 4: DSP Software
- 5: Linear Systems
- 6: Convolution
- 7: Properties of Convolution
- 8: The Discrete Fourier Transform
- 9: Applications of the DFT
- 10: Fourier Transform Properties
- 11: Fourier Transform Pairs
- 12: The Fast Fourier Transform
- 13: Continuous Signal Processing
- 14: Introduction to Digital Filters
- 15: Moving Average Filters
- 16: Windowed-Sinc Filters
- 17: Custom Filters
- 18: FFT Convolution
- 19: Recursive Filters
- 20: Chebyshev Filters
- 21: Filter Comparison
- 22: Audio Processing
- 23: Image Formation & Display
- 24: Linear Image Processing
- 25: Special Imaging Techniques
- 26: Neural Networks (and more!)
- 27: Data Compression
- 28: Digital Signal Processors
- 29: Getting Started with DSPs
- 30: Complex Numbers
- 31: The Complex Fourier Transform
- 32: The Laplace Transform
- 33: The z-Transform
- 34: Explaining Benford's Law
How to order your own hardcover copy
Wouldn't you rather have a bound book instead of 640 loose pages?Your laser printer will thank you!
Order from Amazon.com.
Chapter 13: Continuous Signal Processing
Continuous signals can be decomposed into scaled and shifted delta functions, just as done with discrete signals. The difference is that the continuous delta function is much more complicated and mathematically abstract than its discrete counterpart. Instead of defining the continuous delta function by what it is, we will define it by the characteristics it has.
A thought experiment will show how this works. Imagine an electronic circuit composed of linear components, such as resistors, capacitors and inductors. Connected to the input is a signal generator that produces various shapes of short pulses. The output of the circuit is connected to an oscilloscope, displaying the waveform produced by the circuit in response to each input pulse. The question we want to answer is: how is the shape of the output pulse related to the characteristics of the input pulse? To simplify the investigation, we will only use input pulses that are much shorter than the output. For instance, if the system responds in milli-seconds, we might use input pulses only a few microseconds in length.
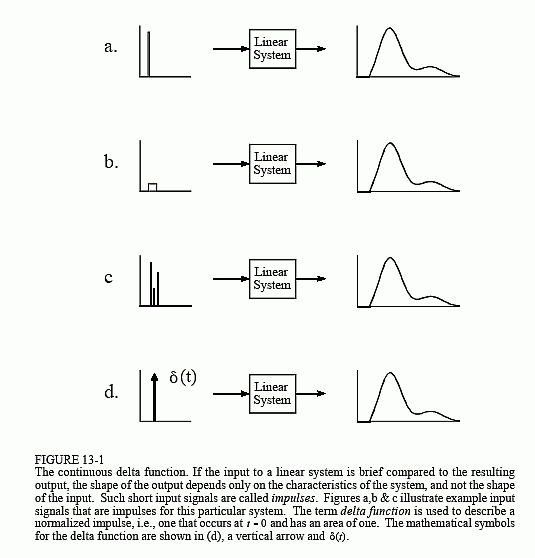
After taking many measurement, we come to three conclusions: First, the shape of the input pulse does not affect the shape of the output signal. This is illustrated in Fig. 13-1, where various shapes of short input pulses produce exactly the same shape of output pulse. Second, the shape of the output waveform is totally determined by the characteristics of the system, i.e., the value and configuration of the resistors, capacitors and inductors. Third, the amplitude of the output pulse is directly proportional to the area of the input pulse. For example, the output will have the same amplitude for inputs of: 1 volt for 1 microsecond, 10 volts for 0.1 microseconds, 1,000 volts for 1 nanosecond, etc. This relationship also allows for input pulses with negative areas. For instance, imagine the combination of a 2 volt pulse lasting 2 microseconds being quickly followed by a -1 volt pulse lasting 4 microseconds. The total area of the input signal is zero, resulting in the output doing nothing.
Input signals that are brief enough to have these three properties are called impulses. In other words, an impulse is any signal that is entirely zero except for a short blip of arbitrary shape. For example, an impulse to a microwave transmitter may have to be in the picosecond range because the electronics responds in nanoseconds. In comparison, a volcano that erupts for years may be a perfectly good impulse to geological changes that take millennia.
Mathematicians don't like to be limited by any particular system, and commonly use the term impulse to mean a signal that is short enough to be an impulse to any possible system. That is, a signal that is infinitesimally narrow. The continuous delta function is a normalized version of this type of impulse. Specifically, the continuous delta function is mathematically defined by three idealized characteristics: (1) the signal must be infinitesimally brief, (2) the pulse must occur at time zero, and (3) the pulse must have an area of one.
Since the delta function is defined to be infinitesimally narrow and have a fixed area, the amplitude is implied to be infinite. Don't let this bother you; it is completely unimportant. Since the amplitude is part of the shape of the impulse, you will never encounter a problem where the amplitude makes any difference, infinite or not. The delta function is a mathematical construct, not a real world signal. Signals in the real world that act as delta functions will always have a finite duration and amplitude.
Just as in the discrete case, the continuous delta function is given the mathematical symbol: δ( ). Likewise, the output of a continuous system in response to a delta function is called the impulse response, and is often denoted by: h( ). Notice that parentheses, ( ), are used to denote continuous signals, as compared to brackets, [ ], for discrete signals. This notation is used in this book and elsewhere in DSP, but isn't universal. Impulses are displayed in graphs as vertical arrows (see Fig. 13-1d), with the length of the arrow indicating the area of the impulse.
To better understand real world impulses, look into the night sky at a planet and a star, for instance, Mars and Sirius. Both appear about the same brightness and size to the unaided eye. The reason for this similarity is not
obvious, since the viewing geometry is drastically different. Mars is about 6000 kilometers in diameter and 60 million kilometers from earth. In comparison, Sirius is about 300 times larger and over one-million times farther away. These dimensions should make Mars appear more than three-thousand times larger than Sirius. How is it possible that they look alike?
These objects look the same because they are small enough to be impulses to the human visual system. The perceived shape is the impulse response of the eye, not the actual image of the star or planet. This becomes obvious when the two objects are viewed through a small telescope; Mars appears as a dim disk, while Sirius still appears as a bright impulse. This is also the reason that stars twinkle while planets do not. The image of a star is small enough that it can be briefly blocked by particles or turbulence in the atmosphere, whereas the larger image of the planet is much less affected.
