The Scientist and Engineer's Guide to
Digital Signal Processing
By Steven W. Smith, Ph.D.
Book Search
Table of contents
- 1: The Breadth and Depth of DSP
- 2: Statistics, Probability and Noise
- 3: ADC and DAC
- 4: DSP Software
- 5: Linear Systems
- 6: Convolution
- 7: Properties of Convolution
- 8: The Discrete Fourier Transform
- 9: Applications of the DFT
- 10: Fourier Transform Properties
- 11: Fourier Transform Pairs
- 12: The Fast Fourier Transform
- 13: Continuous Signal Processing
- 14: Introduction to Digital Filters
- 15: Moving Average Filters
- 16: Windowed-Sinc Filters
- 17: Custom Filters
- 18: FFT Convolution
- 19: Recursive Filters
- 20: Chebyshev Filters
- 21: Filter Comparison
- 22: Audio Processing
- 23: Image Formation & Display
- 24: Linear Image Processing
- 25: Special Imaging Techniques
- 26: Neural Networks (and more!)
- 27: Data Compression
- 28: Digital Signal Processors
- 29: Getting Started with DSPs
- 30: Complex Numbers
- 31: The Complex Fourier Transform
- 32: The Laplace Transform
- 33: The z-Transform
- 34: Explaining Benford's Law
How to order your own hardcover copy
Wouldn't you rather have a bound book instead of 640 loose pages?Your laser printer will thank you!
Order from Amazon.com.
Chapter 34: Explaining Benford's Law
The previous section describes the Ones Scaling Test in terms of statistics, i.e., the analysis of actual numbers. Our task now is to rewrite this test in terms of probability, the underlying mathematics that govern how the numbers are generated.
As discussed in Chapter 2, the mathematical description of a process that generates numbers is called the probability density function, or pdf. In general, there are two ways that the shape of a particular pdf can be known. First, we can understand the physical process that generates the numbers. For instance, the random number generator of a computer falls in this category. We know what the pdf is, because it was specifically designed to have this pdf by the programer that developed the routine.
Second, we can estimate the pdf by examining the generated values. The income tax return numbers are an example of this. It seems unlikely that anyone could mathematically understand or predict the pdf of these numbers; the processes involved are just too complicated. However, we can take a large group of these numbers and form a histogram of their values. This histogram gives us an estimate of the underlying pdf, but isn't exact because of random statistical variations. As the number of samples in the histogram becomes larger, and the width of the bins is made smaller, the accuracy of the estimate becomes better.
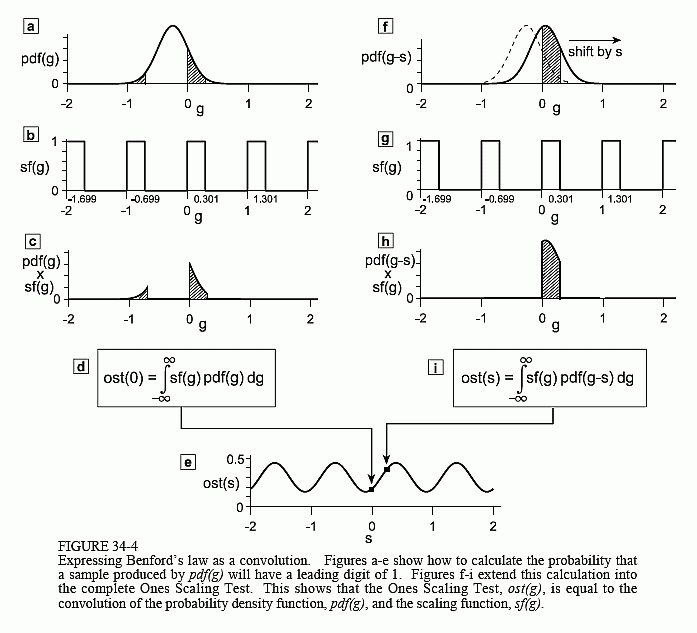
The statistical version of the Ones Scaling Test analyzes a group of numbers. Moving into the world of probability, we will replace this group of numbers with its probability density function. The pdf we will use as an example is shown in Fig. 34-4a. The mathematical name we will give this example curve is pdf(g). However, there is an important catch here; we are representing this probability density function along the base-ten logarithmic number line, rather than the conventional linear number line. The position along the logarithmic axis will be denoted by the variable, g. For instance, g = -2 corresponds to a value of 0.01 on the linear scale, since log(0.01) = -2. Likewise, g = 0 corresponds to 1, g = 1 corresponds to 10, and so on.
Many science and engineering graphs are presented with a logarithmic x-axis, so this probably isn't a new concept for you. However, a special problem arises when converting a probability density function from the linear to the logarithmic number line. The usual way of moving between these domains is simple point-to-point mapping. That is, whatever value is at 0.01 on the linear scale becomes the value at -2 on the log scale; whatever value is at 10 on the linear scale becomes the value at 1 on the log scale, and so on. However, the pdf has a special property that must be taken into account. For instance, suppose we know the shape of a pdf and want to determine how many of the numbers it generates are greater than 3 but less than 4. From basic probability, this fraction is equal to the area under the curve between the values of 3 and 4. Now look at what happens in a point-to-point mapping. The locations of 3 and 4 on the linear scale become log(3) = 0.477 and log(4) = 0.602, respectively, on the log scale. That is, the distance between the two points is 1.00 on the linear scale, but only 0.125 on the logarithmic number line. This changes the area under the curve between the two points, which is simply not acceptable for a pdf.
Fortunately, this is quite simple to correct. First, transfer the pdf from the linear scale to the log scale by using a point-to-point mapping. Second, multiply this mapped curve by the following exponential function to correct the area problem:
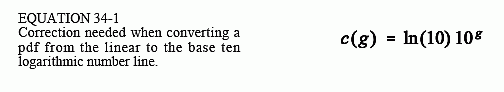
There is also another way to look at this issue. A histogram is created for a group of number by breaking the linear number line into equally spaced bins. But how would this histogram be created on the logarithmic scale? There are two choices. First, you could calculate the histogram on the linear scale, and then transfer the value of the bins to the log scale. However, the equally spaced bins on the linear scale become unequally spaced on the log scale, and Eq. 34-1 would be needed as a correction. Second, you could break the logarithmic number line in equally spaced bins, and directly fill up these bins with the data. This procedure accurately estimates the pdf on the log scale without any additional corrections.
Now back to Fig. 34-4a. The example shown is a Gaussian (normal) curve with a mean of -0.25 and a standard deviation of 0.25, measured on the base ten logarithmic number line. Since it is a normal distribution when displayed on the logarithmic scale, it is given the special name: log-normal. When this pdf is displayed on the linear scale it looks entirely different, as we will see shortly. About 95% of the numbers generated from a normal distribution lie within +/- 2 standard deviations of the mean, or in this example, from -0.75 to 0.250, on the log scale. Converting back to the linear scale, this particular random process will generate 95% of its samples between 10-0.75 and 100.25, that is, between 0.178 and 1.778.
The important point is that this is a single process that generates numbers, but we can look at those numbers on either the linear or the logarithmic scale. For instance, on the linear scale the numbers might look like: 1.2034, 0.3456, 0.9643, 1.8567, and so on. On the log scale these same numbers would be log(1.2034) = 0.0804, -0.4614, -0.0158, 0.2687, respectively. When we ask if this distribution follows Benford's law, we are referring to the numbers on the linear scale. That is, we are looking at the leading digits of 1.2034, 0.3456, 0.9643, 1.8567, etc. However, to understand why Benford's law is being followed or not followed, we will find it necessary to work with their logarithmic counterparts.
The next step is to determine what fraction of samples produced by this pdf have 1 as their leading digit. On the linear number line there are only certain regions where a leading digit of 1 is produced, such as: 0.1 to 0.199999; 1 to 1.99999; 10 to 19.9999; and so on. The corresponding locations on the base ten log scale are: -1.000 to -0.699; 0.000 to 0.301; and 1.000 to 1.301, respectively. In Fig. 34-4b these regions have been marked with a value of one, while all other sections of the logarithmic number line are given a value of zero. This allows the waveform in Fig. (b) to be used as a sampling function, and therefore we will call it, sf(g). Here is how it works. We multiply pdf(g) by sf(g) and display the result in Fig. (c). As shown, this isolates those sections of the pdf where 1 is the leading digit. We then find the total area of these regions by integrating from negative to positive infinity. Now you can see one reason this analysis is carried out on the logarithmic number line: the sampling function is a simple periodic pattern of pulses. In comparison, think about how this sampling function would appear on the linear scale– far too complicated to even consider.
The above procedure is expressed by the equation in (d), which calculates the fraction of number produced by the distribution with 1 as the leading digit. However, as before, even if this number is exactly 0.301, it would not be conclusive proof that the pdf follows Benford's law. To show this we must conduct the Ones Scaling Test. That is, we will adjust pdf(g) such that the numbers it produces are multiplied by a constant that is slightly above unity. We then recalculate the fraction of ones in the leading digit position, and repeat the process many times.
Here we find a second reason to use the logarithmic scale: multiplication on the linear number line becomes addition in the logarithmic domain. On the linear scale we calculate: n x 1.01, while on the logarithmic scale this becomes: log(n) + log(1.01). In other words, on the logarithmic number line we scale the distribution by adding a small constant to each number that is produced. This has the effect of shifting the entire pdf(g) curve to the right a small distance, which we represent by the variable, s. This is shown in Fig. (f). Mathematically, shifting the signal pdf(g) to the right a distance, s, is written pdf(g-s).
The sampling function in Fig. (g) is the same as before; however, it now isolates a different section of the pdf, shown in (h). The integration also goes on as before, with the addition of the shift, s, represented in the equation. In short, we have derived an equation that provides the probability that a number produced by pdf(g) will have 1 in the leading digit position, for any scaling factor, s. As before, we will call this the Ones Scaling Test, and denote it by ost(s). This equation is given in (i), and reprinted below:

The signal ost(s) is nothing more than a continuous version of the graphs shown in Fig. 34-3. If pdf(g) follows Benford's law, then ost(s) will be approximately a constant value of 0.301. If ost(s) deviates from this key value, Benford's law is not being followed. For instance, we can easily see from Fig. (e) that the example pdf in (a) does not follow the law.
These last steps and Eq. 34-2 should look very familiar: shift, multiply, integrate. That's convolution! Comparing Eq. 34-2 with the definition
of convolution (Eq. 13-1 in chapter 13), we have succeeded in expressing Benford's law as a straightforward linear system:

There are two small issues that need to be mentioned in this equation. First, the negative sign in pdf(-g). As you recall, convolution requires that one of the two original signals be flipped left-or-right before the shift, multiply, integrate operations. This is needed for convolution to properly represent linear system theory. On the other hand, this flip not needed in examining Benford's law; it's just a nuisance. Nevertheless, we need to account for it somewhere. In Eq. 34-3 we account for it by pre-flipping pdf(g) by making it pdf(-g). This pre-flip cancels the flip inherent in convolution, keeping the math straight. However, the whole issue of using pdf(-g) instead of pdf(g) is unimportant for Benford's law; it disappears completely in the next step.
The second small issue is a signal processing notation, the elimination of the variable, s. In Fig. 3-4 we write pdf(g) and sf(g), meaning that these two signals have the logarithmic number line as their independent variable, g. However, the Ones Scaling Test is written ost(s), where s is a shift along the logarithmic number line. This distinction between g and s is needed in the derivation to understand how the three signals are related. However, when we get to the shorthand notation of Eq. 34-3, we eliminate s by changing ost(s) to ost(g). This places the three signals, pdf(g), sf(g) and ost(g) all on equal footing, each running along the logarithmic number line.
