The Scientist and Engineer's Guide to
Digital Signal Processing
By Steven W. Smith, Ph.D.
Book Search
Table of contents
- 1: The Breadth and Depth of DSP
- 2: Statistics, Probability and Noise
- 3: ADC and DAC
- 4: DSP Software
- 5: Linear Systems
- 6: Convolution
- 7: Properties of Convolution
- 8: The Discrete Fourier Transform
- 9: Applications of the DFT
- 10: Fourier Transform Properties
- 11: Fourier Transform Pairs
- 12: The Fast Fourier Transform
- 13: Continuous Signal Processing
- 14: Introduction to Digital Filters
- 15: Moving Average Filters
- 16: Windowed-Sinc Filters
- 17: Custom Filters
- 18: FFT Convolution
- 19: Recursive Filters
- 20: Chebyshev Filters
- 21: Filter Comparison
- 22: Audio Processing
- 23: Image Formation & Display
- 24: Linear Image Processing
- 25: Special Imaging Techniques
- 26: Neural Networks (and more!)
- 27: Data Compression
- 28: Digital Signal Processors
- 29: Getting Started with DSPs
- 30: Complex Numbers
- 31: The Complex Fourier Transform
- 32: The Laplace Transform
- 33: The z-Transform
- 34: Explaining Benford's Law
How to order your own hardcover copy
Wouldn't you rather have a bound book instead of 640 loose pages?Your laser printer will thank you!
Order from Amazon.com.
Chapter 5: Linear Systems
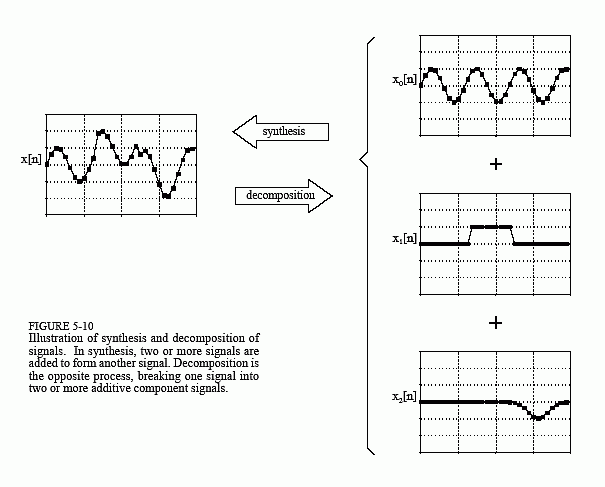
When we are dealing with linear systems, the only way signals can be combined is by scaling (multiplication of the signals by constants) followed by addition. For instance, a signal cannot be multiplied by another signal. Figure 5-10 shows an example: three signals: x0[n], x1[n], and x2[n] are added to form a fourth signal, x[n]. This process of combining signals through scaling and addition is called synthesis.
Decomposition is the inverse operation of synthesis, where a single signal is broken into two or more additive components. This is more involved than synthesis, because there are infinite possible decompositions for any given signal. For example, the numbers 15 and 25 can only be synthesized (added) into the number 40. In comparison, the number 40 can be decomposed into: 1 + 39 or 2 + 38 or -30.5 + 60 + 10.5, etc.
Now we come to the heart of DSP: superposition, the overall strategy for understanding how signals and systems can be analyzed. Consider an input
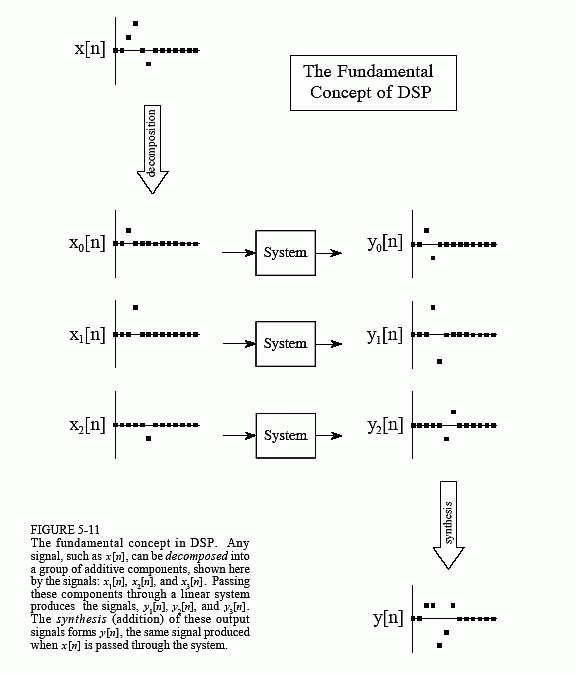
signal, called x[n], passing through a linear system, resulting in an output signal, y[n]. As illustrated in Fig. 5-11, the input signal can be decomposed into a group of simpler signals: x0[n], x1[n], x2[n], etc. We will call these the input signal components. Next, each input signal component is individually passed through the system, resulting in a set of output signal components: y0[n], y1[n], y2[n], etc. These output signal components are then synthesized into the output signal, y[n].
Here is the important part: the output signal obtained by this method is identical to the one produced by directly passing the input signal through the system. This is a very powerful idea. Instead of trying to understanding how complicated signals are changed by a system, all we need to know is how simple signals are modified. In the jargon of signal processing, the input and output signals are viewed as a superposition (sum) of simpler waveforms. This is the basis of nearly all signal processing techniques.
As a simple example of how superposition is used, multiply the number 2041 by the number 4, in your head. How did you do it? You might have imagined 2041 match sticks floating in your mind, quadrupled the mental image, and started counting. Much more likely, you used superposition to simplify the problem. The number 2041 can be decomposed into: 2000 + 40 + 1. Each of these components can be multiplied by 4 and then synthesized to find the final answer, i.e., 8000 + 160 + 4 = 8164.
