The Scientist and Engineer's Guide to
Digital Signal Processing
By Steven W. Smith, Ph.D.
Book Search
Table of contents
- 1: The Breadth and Depth of DSP
- 2: Statistics, Probability and Noise
- 3: ADC and DAC
- 4: DSP Software
- 5: Linear Systems
- 6: Convolution
- 7: Properties of Convolution
- 8: The Discrete Fourier Transform
- 9: Applications of the DFT
- 10: Fourier Transform Properties
- 11: Fourier Transform Pairs
- 12: The Fast Fourier Transform
- 13: Continuous Signal Processing
- 14: Introduction to Digital Filters
- 15: Moving Average Filters
- 16: Windowed-Sinc Filters
- 17: Custom Filters
- 18: FFT Convolution
- 19: Recursive Filters
- 20: Chebyshev Filters
- 21: Filter Comparison
- 22: Audio Processing
- 23: Image Formation & Display
- 24: Linear Image Processing
- 25: Special Imaging Techniques
- 26: Neural Networks (and more!)
- 27: Data Compression
- 28: Digital Signal Processors
- 29: Getting Started with DSPs
- 30: Complex Numbers
- 31: The Complex Fourier Transform
- 32: The Laplace Transform
- 33: The z-Transform
- 34: Explaining Benford's Law
How to order your own hardcover copy
Wouldn't you rather have a bound book instead of 640 loose pages?Your laser printer will thank you!
Order from Amazon.com.
Chapter 18: FFT Convolution
When is FFT convolution faster than standard convolution? The answer depends on the length of the filter kernel, as shown in Fig. 18-3. The time

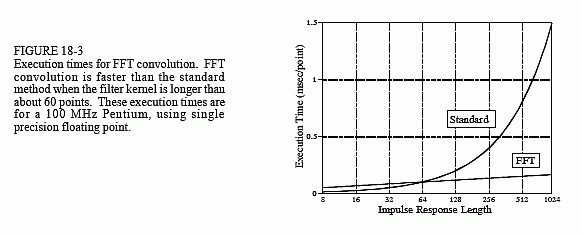
filter kernel. The crossover occurs when the filter kernel has about 40 to 80 samples (depending on the particular hardware used).
The important idea to remember: filter kernels shorter than about 60 points can be implemented faster with standard convolution, and the execution time is proportional to the kernel length. Longer filter kernels can be implemented faster with FFT convolution. With FFT convolution, the filter kernel can be made as long as you like, with very little penalty in execution time. For instance, a 16,000 point filter kernel only requires about twice as long to execute as one with only 64 points.
The speed of the convolution also dictates the precision of the calculation (just as described for the FFT in Chapter 12). This is because the round-off error in the output signal depends on the total number of calculations, which is directly proportional to the computation time. If the output signal is calculated faster, it will also be calculated more precisely. For instance, imagine convolving a signal with a 1000 point filter kernel, with single precision floating point. Using standard convolution, the typical round-off noise can be expected to be about 1 part in 20,000 (from the guidelines in Chapter 4). In comparison, FFT convolution can be expected to be an order of magnitude faster, and an order of magnitude more precise (i.e., 1 part in 200,000).
Keep FFT convolution tucked away for when you have a large amount of data to process and need an extremely long filter kernel. Think in terms of a million sample signal and a thousand point filter kernel. Anything less won't justify the extra programming effort. Don't want to write your own FFT convolution routine? Look in software libraries and packages for prewritten code. Start with this book's web site (see the copyright page).
