The Scientist and Engineer's Guide to
Digital Signal Processing
By Steven W. Smith, Ph.D.
Book Search
Table of contents
- 1: The Breadth and Depth of DSP
- 2: Statistics, Probability and Noise
- 3: ADC and DAC
- 4: DSP Software
- 5: Linear Systems
- 6: Convolution
- 7: Properties of Convolution
- 8: The Discrete Fourier Transform
- 9: Applications of the DFT
- 10: Fourier Transform Properties
- 11: Fourier Transform Pairs
- 12: The Fast Fourier Transform
- 13: Continuous Signal Processing
- 14: Introduction to Digital Filters
- 15: Moving Average Filters
- 16: Windowed-Sinc Filters
- 17: Custom Filters
- 18: FFT Convolution
- 19: Recursive Filters
- 20: Chebyshev Filters
- 21: Filter Comparison
- 22: Audio Processing
- 23: Image Formation & Display
- 24: Linear Image Processing
- 25: Special Imaging Techniques
- 26: Neural Networks (and more!)
- 27: Data Compression
- 28: Digital Signal Processors
- 29: Getting Started with DSPs
- 30: Complex Numbers
- 31: The Complex Fourier Transform
- 32: The Laplace Transform
- 33: The z-Transform
- 34: Explaining Benford's Law
How to order your own hardcover copy
Wouldn't you rather have a bound book instead of 640 loose pages?Your laser printer will thank you!
Order from Amazon.com.
Chapter 9: Applications of the DFT
It is very common for information to be encoded in the sinusoids that form a signal. This is true of naturally occurring signals, as well as those that have been created by humans. Many things oscillate in our universe. For example, speech is a result of vibration of the human vocal cords; stars and planets change their brightness as they rotate on their axes and revolve around each other; ship's propellers generate periodic displacement of the water, and so on. The shape of the time domain waveform is not important in these signals; the key information is in the frequency, phase and amplitude of the component sinusoids. The DFT is used to extract this information.
An example will show how this works. Suppose we want to investigate the sounds that travel through the ocean. To begin, a microphone is placed in the water and the resulting electronic signal amplified to a reasonable level, say a few volts. An analog low-pass filter is then used to remove all frequencies above 80 hertz, so that the signal can be digitized at 160 samples per second. After acquiring and storing several thousand samples, what next?
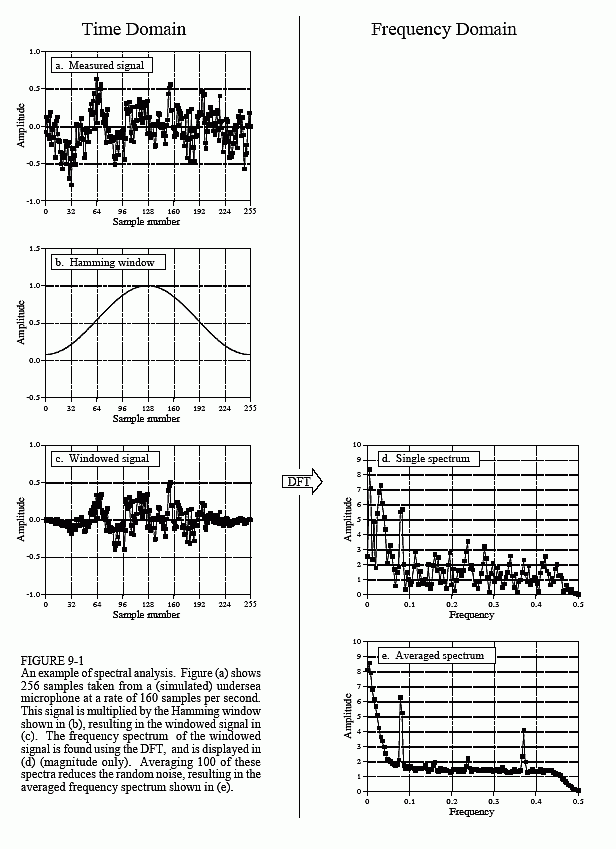
The first thing is to simply look at the data. Figure 9-1a shows 256 samples from our imaginary experiment. All that can be seen is a noisy waveform that conveys little information to the human eye. For reasons explained shortly, the next step is to multiply this signal by a smooth curve called a Hamming window, shown in (b). (Chapter 16 provides the equations for the Hamming and other windows; see Eqs. 16-1 and 16-2, and Fig. 16-2a). This results in a 256 point signal where the samples near the ends have been reduced in amplitude, as shown in (c).
Taking the DFT, and converting to polar notation, results in the 129 point frequency spectrum in (d). Unfortunately, this also looks like a noisy mess. This is because there is not enough information in the original 256 points to obtain a well behaved curve. Using a longer DFT does nothing to help this problem. For example, if a 2048 point DFT is used, the frequency spectrum becomes 1025 samples long. Even though the original 2048 points contain more information, the greater number of samples in the spectrum dilutes the information by the same factor. Longer DFTs provide better frequency resolution, but the same noise level.
The answer is to use more of the original signal in a way that doesn't increase the number of points in the frequency spectrum. This can be done by breaking the input signal into many 256 point segments. Each of these segments is multiplied by the Hamming window, run through a 256 point DFT, and converted to polar notation. The resulting frequency spectra are then averaged to form a single 129 point frequency spectrum. Figure (e) shows an example of averaging 100 of the frequency spectra typified by (d). The improvement is obvious; the noise has been reduced to a level that allows interesting features of the signal to be observed. Only the magnitude of the frequency domain is averaged in this manner; the phase is usually discarded because it doesn't contain useful information. The random noise reduces in proportion to the square-root of the number of segments. While 100 segments is typical, some applications might average millions of segments to bring out weak features.
There is also a second method for reducing spectral noise. Start by taking a very long DFT, say 16,384 points. The resulting frequency spectrum is high resolution (8193 samples), but very noisy. A low-pass digital filter is then used to smooth the spectrum, reducing the noise at the expense of the resolution. For example, the simplest digital filter might average 64 adjacent samples in the original spectrum to produce each sample in the filtered spectrum. Going through the calculations, this provides about the same noise and resolution as the first method, where the 16,384 points would be broken into 64 segments of 256 points each.
Which method should you use? The first method is easier, because the digital filter isn't needed. The second method has the potential of better performance, because the digital filter can be tailored to optimize the trade-off between noise and resolution. However, this improved performance is seldom worth the trouble. This is because both noise and resolution can be improved by using more data from the input signal. For example,
imagine breaking the acquired data into 10,000 segments of 16,384 samples each. This resulting frequency spectrum is high resolution (8193 points) and low noise (10,000 averages). Problem solved! For this reason, we will only look at the averaged segment method in this discussion.
Figure 9-2 shows an example spectrum from our undersea microphone, illustrating the features that commonly appear in the frequency spectra of acquired signals. Ignore the sharp peaks for a moment. Between 10 and 70 hertz, the signal consists of a relatively flat region. This is called white noise because it contains an equal amount of all frequencies, the same as white light. It results from the noise on the time domain waveform being uncorrelated from sample-to-sample. That is, knowing the noise value present on any one sample provides no information on the noise value present on any other sample. For example, the random motion of electrons in electronic circuits produces white noise. As a more familiar example, the sound of the water spray hitting the shower floor is white noise. The white noise shown in Fig. 9-2 could be originating from any of several sources, including the analog electronics, or the ocean itself.
Above 70 hertz, the white noise rapidly decreases in amplitude. This is a result of the roll-off of the antialias filter. An ideal filter would pass all frequencies below 80 hertz, and block all frequencies above. In practice, a perfectly sharp cutoff isn't possible, and you should expect to see this gradual drop. If you don't, suspect that an aliasing problem is present.
Below about 10 hertz, the noise rapidly increases due to a curiosity called 1/f noise (one-over-f noise). 1/f noise is a mystery. It has been measured in very diverse systems, such as traffic density on freeways and electronic noise in transistors. It probably could be measured in all systems, if you look low enough in frequency. In spite of its wide occurrence, a general theory and understanding of 1/f noise has eluded researchers. The cause of this noise can be identified in some specific systems; however, this doesn't answer the question of why 1/f noise is everywhere. For common analog electronics and most physical systems, the transition between white noise and 1/f noise occurs between about 1 and 100 hertz.
Now we come to the sharp peaks in Fig. 9-2. The easiest to explain is at 60 hertz, a result of electromagnetic interference from commercial electrical power. Also expect to see smaller peaks at multiples of this frequency (120, 180, 240 hertz, etc.) since the power line waveform is not a perfect sinusoid. It is also common to find interfering peaks between 25-40 kHz, a favorite for designers of switching power supplies. Nearby radio and television stations produce interfering peaks in the megahertz range. Low frequency peaks can be caused by components in the system vibrating when shaken. This is called microphonics, and typically creates peaks at 10 to 100 hertz.
Now we come to the actual signals. There is a strong peak at 13 hertz, with weaker peaks at 26 and 39 hertz. As discussed in the next chapter, this is the frequency spectrum of a nonsinusoidal periodic waveform. The peak at 13 hertz is called the fundamental frequency, while the peaks at 26 and 39
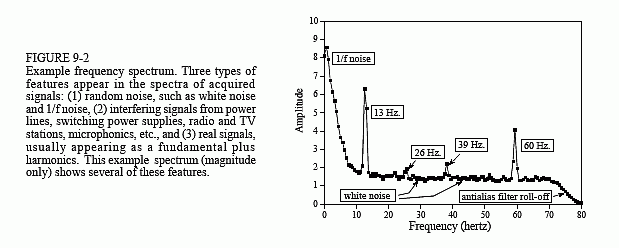
hertz are referred to as the second and third harmonic respectively. You would also expect to find peaks at other multiples of 13 hertz, such as 52, 65, 78 hertz, etc. You don't see these in Fig. 9-2 because they are buried in the white noise. This 13 hertz signal might be generated, for example, by a submarines's three bladed propeller turning at 4.33 revolutions per second. This is the basis of passive sonar, identifying undersea sounds by their frequency and harmonic content.
Suppose there are peaks very close together, such as shown in Fig. 9-3. There are two factors that limit the frequency resolution that can be obtained, that is, how close the peaks can be without merging into a single entity. The first factor is the length of the DFT. The frequency spectrum produced by an N point DFT consists of N/2 + 1 samples equally spaced between zero and one-half of the sampling frequency. To separate two closely spaced frequencies, the sample spacing must be smaller than the distance between the two peaks. For example, a 512 point DFT is sufficient to separate the peaks in Fig. 9-3, while a 128 point DFT is not.
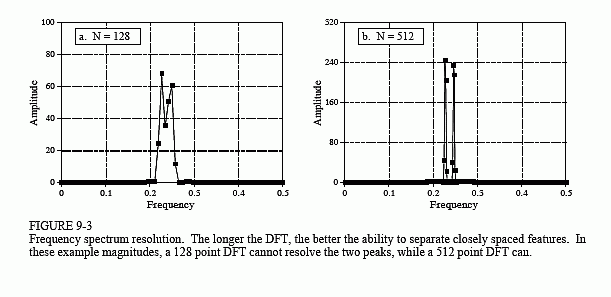
The second factor limiting resolution is more subtle. Imagine a signal created by adding two sine waves with only a slight difference in their frequencies. Over a short segment of this signal, say a few periods, the waveform will look like a single sine wave. The closer the frequencies, the longer the segment must be to conclude that more than one frequency is present. In other words, the length of the signal limits the frequency resolution. This is distinct from the first factor, because the length of the input signal does not have to be the same as the length of the DFT. For example, a 256 point signal could be padded with zeros to make it 2048 points long. Taking a 2048 point DFT produces a frequency spectrum with 1025 samples. The added zeros don't change the shape of the spectrum, they only provide more samples in the frequency domain. In spite of this very close sampling, the ability to separate closely spaced peaks would be only slightly better than using a 256 point DFT. When the DFT is the same length as the input signal, the resolution is limited about equally by these two factors. We will come back to this issue shortly.
Next question: What happens if the input signal contains a sinusoid with a frequency between two of the basis functions? Figure 9-4a shows the answer. This is the frequency spectrum of a signal composed of two sine waves, one having a frequency matching a basis function, and the other with a frequency between two of the basis functions. As you should expect, the first sine wave is represented as a single point. The other peak is more difficult to understand. Since it cannot be represented by a single sample, it becomes a peak with tails that extend a significant distance away.
The solution? Multiply the signal by a Hamming window before taking the DFT, as was previously discussed. Figure (b) shows that the spectrum is changed in three ways by using the window. First, the two peaks are made to look more alike. This is good. Second, the tails are greatly reduced.
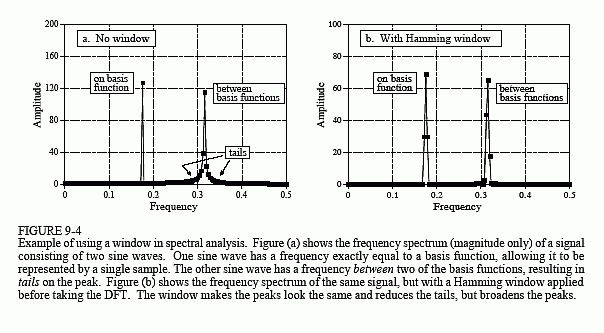
This is also good. Third, the window reduces the resolution in the spectrum by making the peaks wider. This is bad. In DSP jargon, windows provide a trade-off between resolution (the width of the peak) and spectral leakage (the amplitude of the tails).
To explore the theoretical aspects of this in more detail, imagine an infinitely long discrete sine wave at a frequency of 0.1 the sampling rate. The frequency spectrum of this signal is an infinitesimally narrow peak, with all other frequencies being zero. Of course, neither this signal nor its frequency spectrum can be brought into a digital computer, because of their infinite and infinitesimal nature. To get around this, we change the signal in two ways, both of which distort the true frequency spectrum.
First, we truncate the information in the signal, by multiplying it by a window. For example, a 256 point rectangular window would allow 256 points to retain their correct value, while all the other samples in the infinitely long signal would be set to a value of zero. Likewise, the Hamming window would shape the retained samples, besides setting all points outside the window to zero. The signal is still infinitely long, but only a finite number of the samples have a nonzero value.
How does this windowing affect the frequency domain? When two time domain signals are multiplied, the corresponding frequency domains are convolved. Since the original spectrum is an infinitesimally narrow peak (i.e., a delta function), the spectrum of the windowed signal is the spectrum of the window shifted to the location of the peak. Figure 9-5 shows how the spectral peak would appear using three different window options. Figure 9-5a results from a rectangular window. Figures (b) and (c) result from using two popular windows, the Hamming and the Blackman (as previously mentioned, see Eqs. 16-1 and 16-2, and Fig. 16-2a for information on these windows).
As shown in Fig. 9-5, all these windows have degraded the original spectrum by broadening the peak and adding tails composed of numerous side lobes. This is an unavoidable result of using only a portion of the original time domain signal. Here we can see the tradeoff between the three windows. The Blackman has the widest main lobe (bad), but the lowest amplitude tails (good). The rectangular window has the narrowest main lobe (good) but the largest tails (bad). The Hamming window sits between these two.
Notice in Fig. 9-5 that the frequency spectra are continuous curves, not discrete samples. After windowing, the time domain signal is still infinitely long, even though most of the samples are zero. This means that the frequency spectrum consists of ∞/2 + 1 samples between 0 and 0.5, which is the same as a continuous line.
This brings in the second way we need to modify the time domain signal to allow it to be represented in a computer: select N points from the signal. These N points must contain all the nonzero points identified by the window, but may also include any number of the zeros. This has the effect
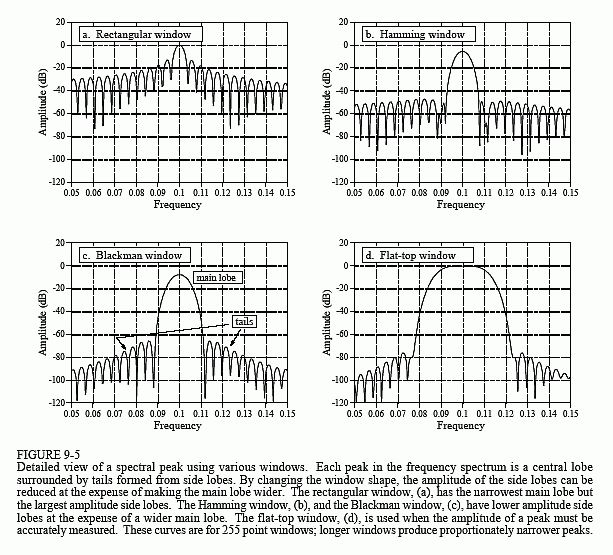
of sampling the frequency spectrum's continuous curve. For example, if N is chosen to be 1024, the spectrum's continuous curve will be sampled 513 times between 0 and 0.5. If N is chosen to be much larger than the window length, the samples in the frequency domain will be close enough that the peaks and valleys of the continuous curve will be preserved in the new spectrum. If N is made the same as the window length, the fewer number of samples in the spectrum results in the regular pattern of peaks and valleys turning into irregular tails, depending on where the samples happen to fall. This explains why the two peaks in Fig. 9-4a do not look alike. Each peak in Fig 9-4a is a sampling of the underlying curve in Fig. 9-5a. The presence or absence of the tails depends on where the samples are taken in relation to the peaks and valleys. If the sine wave exactly matches a basis function, the samples occur exactly at the valleys, eliminating the tails. If the sine wave is between two basis functions, the samples occur somewhere along the peaks and valleys, resulting in various patterns of tails.
This leads us to the flat-top window, shown in Fig. 9-5d. In some applications the amplitude of a spectral peak must be measured very accurately. Since the DFT?s frequency spectrum is formed from samples, there is nothing to guarantee that a sample will occur exactly at the top of a peak. More than likely, the nearest sample will be slightly off-center, giving a value lower than the true amplitude. The solution is to use a window that produces a spectral peak with a flat top, insuring that one or more of the samples will always have the correct peak value. As shown in Fig. 9-5d, the penalty for this is a very broad main lobe, resulting in poor frequency resolution.
As it turns out, the shape we want for a flat-top window is exactly the same shape as the filter kernel of a low-pass filter. We will discuss the theoretical reasons for this in later chapters; for now, here is a cookbook description of how the technique is used. Chapter 16 discusses a low-pass filter called the windowed-sinc. Equation 16-4 describes how to generate the filter kernel (which we want to use as a window), and Fig. 16-4a illustrates the typical shape of the curve. To use this equation, you will need to know the value of two parameters: M and fc. These are found from the relations: M = N-2, and fc = s/N, where N is the length of the DFT being used, and s is the number of samples you want on the flat portion of the peak (usually between 3 and 5). Table 16-1 shows a program for calculating the filter kernel (our window), including two subtle features: the normalization constant, K, and how to avoid a divide-by-zero error on the center sample. When using this method, remember that a DC value of one in the time domain will produce a peak of amplitude one in the frequency domain. However, a sinusoid of amplitude one in the time domain will only produce a spectral peak of amplitude one-half. (This is discussed in the last chapter: Synthesis, Calculating the Inverse DFT).
