The Scientist and Engineer's Guide to
Digital Signal Processing
By Steven W. Smith, Ph.D.
Book Search
Table of contents
- 1: The Breadth and Depth of DSP
- 2: Statistics, Probability and Noise
- 3: ADC and DAC
- 4: DSP Software
- 5: Linear Systems
- 6: Convolution
- 7: Properties of Convolution
- 8: The Discrete Fourier Transform
- 9: Applications of the DFT
- 10: Fourier Transform Properties
- 11: Fourier Transform Pairs
- 12: The Fast Fourier Transform
- 13: Continuous Signal Processing
- 14: Introduction to Digital Filters
- 15: Moving Average Filters
- 16: Windowed-Sinc Filters
- 17: Custom Filters
- 18: FFT Convolution
- 19: Recursive Filters
- 20: Chebyshev Filters
- 21: Filter Comparison
- 22: Audio Processing
- 23: Image Formation & Display
- 24: Linear Image Processing
- 25: Special Imaging Techniques
- 26: Neural Networks (and more!)
- 27: Data Compression
- 28: Digital Signal Processors
- 29: Getting Started with DSPs
- 30: Complex Numbers
- 31: The Complex Fourier Transform
- 32: The Laplace Transform
- 33: The z-Transform
- 34: Explaining Benford's Law
How to order your own hardcover copy
Wouldn't you rather have a bound book instead of 640 loose pages?Your laser printer will thank you!
Order from Amazon.com.
Chapter 4: DSP Software
The encoding scheme for floating point numbers is more complicated than for fixed point. The basic idea is the same as used in scientific notation, where a mantissa is multiplied by ten raised to some exponent. For instance, 5.4321 × 106, where 5.4321 is the mantissa and 6 is the exponent. Scientific notation is exceptional at representing very large and very small numbers. For example: 1.2 × 1050, the number of atoms in the earth, or 2.6 × 10-23, the distance a turtle crawls in one second, compared to the diameter of our galaxy. Notice that numbers represented in scientific notation are normalized so that there is only a single nonzero digit left of the decimal point. This is achieved by adjusting the exponent as needed.
Floating point representation is similar to scientific notation, except everything is carried out in base two, rather than base ten. While several similar formats are in use, the most common is ANSI/IEEE Std. 754-1985. This standard defines the format for 32 bit numbers called single precision, as well as 64 bit numbers called double precision. As shown in Fig. 4-2, the 32 bits used in single precision are divided into three separate groups: bits 0 through 22 form the mantissa, bits 23 through 30 form the exponent, and bit 31 is the sign bit. These bits form the floating point number, v, by the following relation:
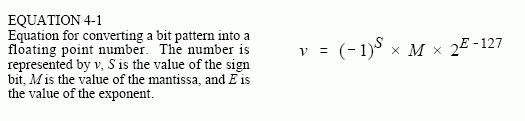
The term: (-1)S, simply means that the sign bit, S, is 0 for a positive number and 1 for a negative number. The variable, E, is the number between 0 and 255 represented by the eight exponent bits. Subtracting 127 from this number allows the exponent term to run from to In other words, the exponent is stored in offset binary with an offset of 127.
The mantissa, M, is formed from the 23 bits as a binary fraction. For example, the decimal fraction: 2.783, is interpreted: 2 + 7/10 + 8/100 + 3/1000. The binary fraction: 1.0101, means: 1 + 0/2 + 1/4 + 0/8 + 1/16. Floating point numbers are normalized in the same way as scientific notation, that is, there is only one nonzero digit left of the decimal point (called a binary point in

base 2). Since the only nonzero number that exists in base two is 1, the leading digit in the mantissa will always be a 1, and therefore does not need to be stored. Removing this redundancy allows the number to have an additional one bit of precision. The 23 stored bits, referred to by the notation: m22,m21,m21,…,m0, form the mantissa according to:
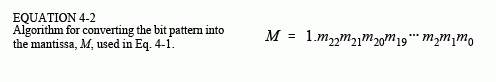
In other words, M = 1 + m222-1 + m212-2 + m202-3…. If bits 0 through 22 are all zeros, M takes on the value of one. If bits 0 through 22 are all ones, M is just a hair under two, i.e., 2-2-23.
Using this encoding scheme, the largest number that can be represented is: ±(2-2-23)×2128 = ±6.8 × 1038. Likewise, the smallest number that can be represented is: ±1.0 × 2-127 = ±5.9 × 10-39. The IEEE standard reduces this range slightly to free bit patterns that are assigned special meanings. In particular, the largest and smallest numbers allowed in the standard are ±3.4 × 1038 and ?1.2 ? 10-38 respectively. The freed bit patterns allow three special classes of numbers: (1) ±0 is defined as all of the mantissa and exponent bits being zero. (2) ±∞ is defined as all of the mantissa bits being zero, and all of the exponent bits being one. (3) A group of very small unnormalized numbers between ?1.2 ? 10-38 and ?1.4 ? 10-45. These are lower precision numbers obtained by removing the requirement that the leading digit in the mantissa be a one. Besides these three special classes, there are bit patterns that are not assigned a meaning, commonly referred to as NANs (Not A Number).
The IEEE standard for double precision simply adds more bits to the single precision format. Of the 64 bits used to store a double precision number, bits 0 through 51 are the mantissa, bits 52 through 62 are the exponent, and bit 63 is the sign bit. As before, the mantissa is between one and just under two, i.e., M = 1 +m512-1 +m502-2 + m492-3…. The 11 exponent bits form a number between 0 and 2047, with an offset of 1023, allowing exponents from 2-1023 to 21024. The largest and smallest numbers allowed are ?1.8 ? 10308 and ?2.2 ? 10-308, respectively. These are incredibly large and small numbers! It is quite uncommon to find an application where single precision is not adequate. You will probably never find a case where double precision limits what you want to accomplish.
