The Scientist and Engineer's Guide to
Digital Signal Processing
By Steven W. Smith, Ph.D.
Book Search
Table of contents
- 1: The Breadth and Depth of DSP
- 2: Statistics, Probability and Noise
- 3: ADC and DAC
- 4: DSP Software
- 5: Linear Systems
- 6: Convolution
- 7: Properties of Convolution
- 8: The Discrete Fourier Transform
- 9: Applications of the DFT
- 10: Fourier Transform Properties
- 11: Fourier Transform Pairs
- 12: The Fast Fourier Transform
- 13: Continuous Signal Processing
- 14: Introduction to Digital Filters
- 15: Moving Average Filters
- 16: Windowed-Sinc Filters
- 17: Custom Filters
- 18: FFT Convolution
- 19: Recursive Filters
- 20: Chebyshev Filters
- 21: Filter Comparison
- 22: Audio Processing
- 23: Image Formation & Display
- 24: Linear Image Processing
- 25: Special Imaging Techniques
- 26: Neural Networks (and more!)
- 27: Data Compression
- 28: Digital Signal Processors
- 29: Getting Started with DSPs
- 30: Complex Numbers
- 31: The Complex Fourier Transform
- 32: The Laplace Transform
- 33: The z-Transform
- 34: Explaining Benford's Law
How to order your own hardcover copy
Wouldn't you rather have a bound book instead of 640 loose pages?Your laser printer will thank you!
Order from Amazon.com.
Chapter 34: Explaining Benford's Law
Frank Benford was a research physicist at General Electric in the 1930s when he noticed something unusual about a book of logarithmic tables. The first pages showed more wear than the last pages, indicating that numbers beginning with the digit 1 were being looked up more often than numbers beginning with 2 through 9. Benford seized upon this idea and spent years collecting data to show that this pattern was widespread in nature. In 1938, Benford published his results, citing more than 20,000 values such as atomic weights, numbers in magazine articles, baseball statistics, and the areas of rivers.
This pattern of numbers is unexpected and counterintuitive. In fact, many do not believe it is real until they conduct an experiment for themselves. I didn't! For instance, go through several pages of today's newspaper and examine the leading digit of each number. That is, start from the left of each number and ignore the sign, the decimal point and any zeros. The first digit you come to, between 1 and 9, is the leading digit. For example, 3 is the leading digit of 37.3447, and 6 is the leading digit of -0.06345. Since there are nine possible digits, you would expect that one-ninth (11.11%) of the numbers would have 1 in the leading digit position. However, this is not what you will find– about 30.1% of the numbers will start with 1. It gets even stranger from here.

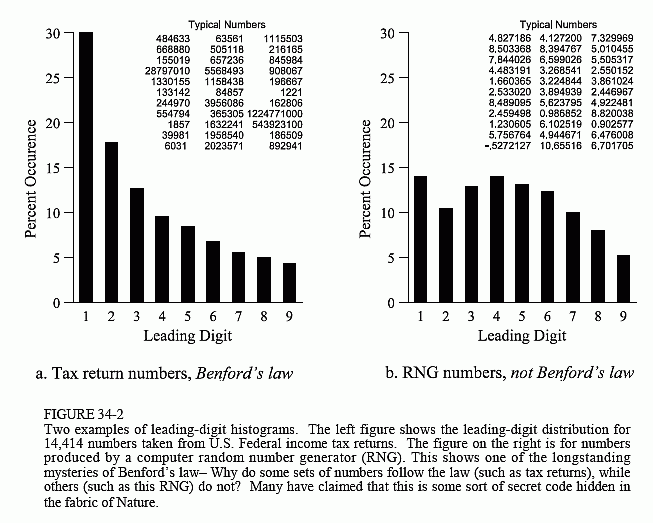
Figure 34-2 shows two examples of Benford's law. The histogram on the left is for 14,414 numbers taken from the income tax returns of U.S. corporations. The pattern here is obvious and very repeatable. The leading digit in these numbers is a 1 about 30.1% of the time, a 2 about 17.6% of the time, and so on. Mathematicians immediately recognize that these values correspond to the spacing on the logarithmic number line. That is, the distance between 1 and 2 on the log scale is log(2) - log(1) = 0.301. The distance between 2 and 3 is log(3) - log(2) = 0.176, and so on. Benford showed us that this logarithmic pattern of leading digits is extremely common in nature and human activities. In fact, even the physical constants of the universe follow this pattern– just look at the tables in a physics textbook.
On the other hand, not all sets of numbers follow Benford's law. For example, the histogram in Fig. 34-2b was generated by taking a large number of samples from a computer random number generator. These particular numbers follow a normal distribution with a mean of five and a standard deviation of three. Changing any of these parameters will drastically change the shape of this histogram, with little apparent rhyme or reason. Obviously, these numbers do not follow the logarithmic leading-digit distribution. Likewise, most of the common distributions you learned about in statistics classes do not follow Benford's law. One of the primary mysteries of Benford's law has been this seemingly unpredictable behavior. Why does one set of numbers follow the logarithmic pattern, while another set of numbers does not?
As if this wasn't mysterious enough, Benford's law has another property that is certain to keep you up at night. Figure 34-2a was created from numbers that appear in U.S. tax returns, and therefore each of these numbers is a dollar value. But what is so special about the U.S. dollar? Suppose that you are a financial expert in India and want to examine this set of data. To make it easier you convert all of the dollar values to Indian rupees by multiplying each number by the current conversion rate. It is likely that the leading digit of all 14,414 numbers will be changed
by this conversion. Nevertheless, about 30.1% of the converted numbers will still have a leading digit of 1. In other words, if a set of numbers follows Benford's law, multiplying the numbers by any possible constant will create another set of numbers that also follows Benford's law. A system that remains unchanged when multiplied by a constant is called scale invariant. Specifically, groups of numbers that follow Benford's law are scale invariant. Likewise, groups of numbers that do not follow Benford's law are not. For instance, this procedure would scramble the shape of the histogram in Fig. 34-2b.
Now suppose that this tax return data is being examined by an alien from another planet. Since he has eight fingers, he converts all of his numbers to base 8. Like before, most or all of the leading digits will change in this procedure. In spite of this, the new group of numbers also follows Benford's law (taking into account that there are no 8's or 9's in base 8). This property is called base invariance. In general, if a group of numbers follows Benford's law in one base, it will also follow Benford's law if converted to another base. However, there are some exceptions to this that we will look at later.
What does this all mean? Over the last seven decades Benford's law has achieved almost a cult following. It has been widely claimed to be evidence of some mysterious or paranormal property of our universe. For instance, Benford himself tried to connect the mathematics with Nature, claiming that mere Man counts arithmetically, 1,2,3,4..., while Nature counts e0, ex, e2x, e3x, and so on. In another popular version, suppose that nature contains some underlying and universal distribution of numbers. Since it is universal, it should look the same regardless of how we choose to examine it. In particular, it should not make any difference what units we associate with the numbers. The distribution should appear the same if we express it in dollars or rupees, feet or meters, Fahrenheit or Celsius, and so on. Likewise, the appearance should not change when we examine the numbers in different bases. It has been mathematically proven that the logarithmic leading-digit pattern is the only distribution that fulfils these invariance requirements. Therefore, if there is an underlying universal distribution, Benford's law must be it. Based on this logic, it is very common to hear that Benford's law only applies to numbers that have units associated with them. On the other end of the spectrum, crackpots abound that associate Benford's law with psychic and other paranormal claims.
Don't waste your time trying to understand the above ideas; they are completely on the wrong track. There is no "universal distribution" and this phenomenon is unrelated to "units". In the end, we will find that Benford's law looks more like a well-executed magic trick than a hidden property of the universe.
