The Scientist and Engineer's Guide to
Digital Signal Processing
By Steven W. Smith, Ph.D.
Book Search
Table of contents
- 1: The Breadth and Depth of DSP
- 2: Statistics, Probability and Noise
- 3: ADC and DAC
- 4: DSP Software
- 5: Linear Systems
- 6: Convolution
- 7: Properties of Convolution
- 8: The Discrete Fourier Transform
- 9: Applications of the DFT
- 10: Fourier Transform Properties
- 11: Fourier Transform Pairs
- 12: The Fast Fourier Transform
- 13: Continuous Signal Processing
- 14: Introduction to Digital Filters
- 15: Moving Average Filters
- 16: Windowed-Sinc Filters
- 17: Custom Filters
- 18: FFT Convolution
- 19: Recursive Filters
- 20: Chebyshev Filters
- 21: Filter Comparison
- 22: Audio Processing
- 23: Image Formation & Display
- 24: Linear Image Processing
- 25: Special Imaging Techniques
- 26: Neural Networks (and more!)
- 27: Data Compression
- 28: Digital Signal Processors
- 29: Getting Started with DSPs
- 30: Complex Numbers
- 31: The Complex Fourier Transform
- 32: The Laplace Transform
- 33: The z-Transform
- 34: Explaining Benford's Law
How to order your own hardcover copy
Wouldn't you rather have a bound book instead of 640 loose pages?Your laser printer will thank you!
Order from Amazon.com.
Chapter 10: Fourier Transform Properties
The Fourier Transform is linear, that is, it possesses the properties of homogeneity and additivity. This is true for all four members of the Fourier transform family (Fourier transform, Fourier Series, DFT, and DTFT).
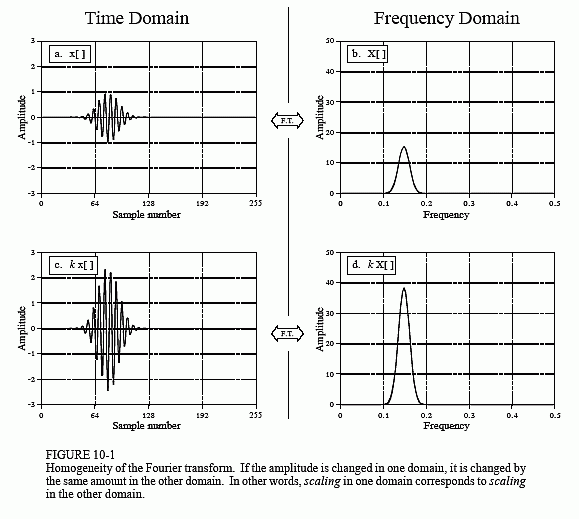
Figure 10-1 provides an example of how homogeneity is a property of the Fourier transform. Figure (a) shows an arbitrary time domain signal, with the corresponding frequency spectrum shown in (b). We will call these two signals: x[ ] and X[ ], respectively. Homogeneity means that a change in amplitude in one domain produces an identical change in amplitude in the other domain. This should make intuitive sense: when the amplitude of a time domain waveform is changed, the amplitude of the sine and cosine waves making up that waveform must also change by an equal amount.
In mathematical form, if x[ ] and X[ ] are a Fourier Transform pair, then kx[ ] and kX[ ] are also a Fourier Transform pair, for any constant k. If the frequency domain is represented in rectangular notation, kX[ ] means that both the real part and the imaginary part are multiplied by k. If the frequency domain is represented in polar notation, kX[ ] means that the magnitude is multiplied by k, while the phase remains unchanged.
Additivity of the Fourier transform means that addition in one domain corresponds to addition in the other domain. An example of this is shown in Fig. 10-2. In this illustration, (a) and (b) are signals in the time domain called x1[n] and x2[n], respectively. Adding these signals produces a third time domain signal called x3[n], shown in (c). Each of these three signals has a frequency spectrum consisting of a real and an imaginary part, shown in (d) through (i). Since the two time domain signals add to produce the third time domain signal, the two corresponding spectra add to produce the third spectrum. Frequency spectra are added in rectangular notation by adding the real parts to the real parts and the imaginary parts to the imaginary parts. If: x1[n] + x2[n] = x3[n], then: ReX1[f] + ReX2[f] = ReX3[f] and ImX1[f] + ImX2[f] = ImX3[f]. Think of this in terms of cosine and sine waves. All the cosine waves add (the real parts) and all the sine waves add (the imaginary parts) with no interaction between the two.
Frequency spectra in polar form cannot be directly added; they must be converted into rectangular notation, added, and then reconverted back to
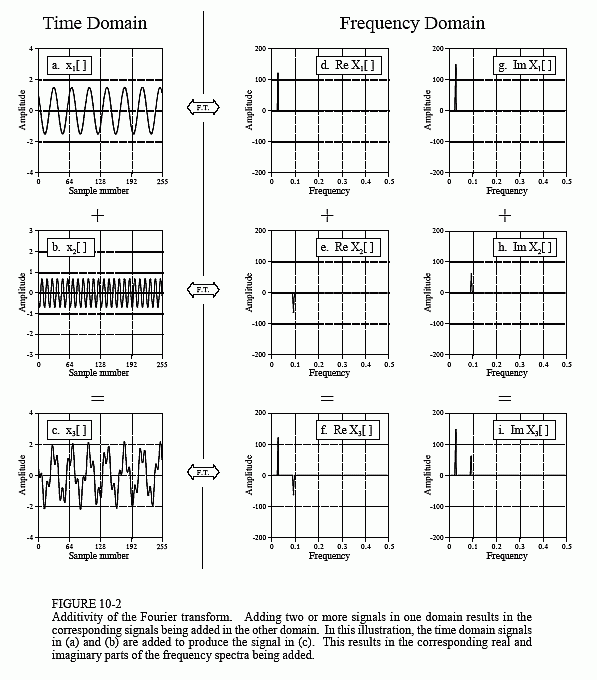
polar form. This can also be understood in terms of how sinusoids behave. Imagine adding two sinusoids having the same frequency, but with different amplitudes (A1 and A2) and phases (φ1 and φ2). If the two phases happen to be same (φ1 = φ2), the amplitudes will add (A1 + A2) when the sinusoids are added. However, if the two phases happen to be exactly opposite (φ1 = -φ2), the amplitudes will subtract (A1 - A2) when the sinusoids are added. The point is, when sinusoids (or spectra) are in polar form, they cannot be added by simply adding the magnitudes and phases.
In spite of being linear, the Fourier transform is not shift invariant. In other words, a shift in the time domain does not correspond to a shift in the frequency domain. This is the topic of the next section.
