The Scientist and Engineer's Guide to
Digital Signal Processing
By Steven W. Smith, Ph.D.
Book Search
Table of contents
- 1: The Breadth and Depth of DSP
- 2: Statistics, Probability and Noise
- 3: ADC and DAC
- 4: DSP Software
- 5: Linear Systems
- 6: Convolution
- 7: Properties of Convolution
- 8: The Discrete Fourier Transform
- 9: Applications of the DFT
- 10: Fourier Transform Properties
- 11: Fourier Transform Pairs
- 12: The Fast Fourier Transform
- 13: Continuous Signal Processing
- 14: Introduction to Digital Filters
- 15: Moving Average Filters
- 16: Windowed-Sinc Filters
- 17: Custom Filters
- 18: FFT Convolution
- 19: Recursive Filters
- 20: Chebyshev Filters
- 21: Filter Comparison
- 22: Audio Processing
- 23: Image Formation & Display
- 24: Linear Image Processing
- 25: Special Imaging Techniques
- 26: Neural Networks (and more!)
- 27: Data Compression
- 28: Digital Signal Processors
- 29: Getting Started with DSPs
- 30: Complex Numbers
- 31: The Complex Fourier Transform
- 32: The Laplace Transform
- 33: The z-Transform
- 34: Explaining Benford's Law
How to order your own hardcover copy
Wouldn't you rather have a bound book instead of 640 loose pages?Your laser printer will thank you!
Order from Amazon.com.
Chapter 14: Introduction to Digital Filters
It may not be obvious why the step response is of such concern in time domain filters. You may be wondering why the impulse response isn't the important parameter. The answer lies in the way that the human mind understands and processes information. Remember that the step, impulse and frequency responses all contain identical information, just in different arrangements. The step response is useful in time domain analysis because it matches the way humans view the information contained in the signals.
For example, suppose you are given a signal of some unknown origin and asked to analyze it. The first thing you will do is divide the signal into regions of similar characteristics. You can't stop from doing this; your mind will do it automatically. Some of the regions may be smooth; others may have large amplitude peaks; others may be noisy. This segmentation is accomplished by identifying the points that separate the regions. This is where the step function comes in. The step function is the purest way of representing a division between two dissimilar regions. It can mark when an event starts, or when an event ends. It tells you that whatever is on the left is somehow different from whatever is on the right. This is how the human mind views time domain information: a group of step functions dividing the information into regions of similar characteristics. The step response, in turn, is important because it describes how the dividing lines are being modified by the filter.
The step response parameters that are important in filter design are shown in Fig. 14-2. To distinguish events in a signal, the duration of the step response must be shorter than the spacing of the events. This dictates that the step response should be as fast (the DSP jargon) as possible. This is shown in Figs. (a) & (b). The most common way to specify the risetime (more jargon) is to quote the number of samples between the 10% and 90% amplitude levels. Why isn't a very fast risetime always possible? There are many reasons, noise reduction, inherent limitations of the data acquisition system, avoiding aliasing, etc.
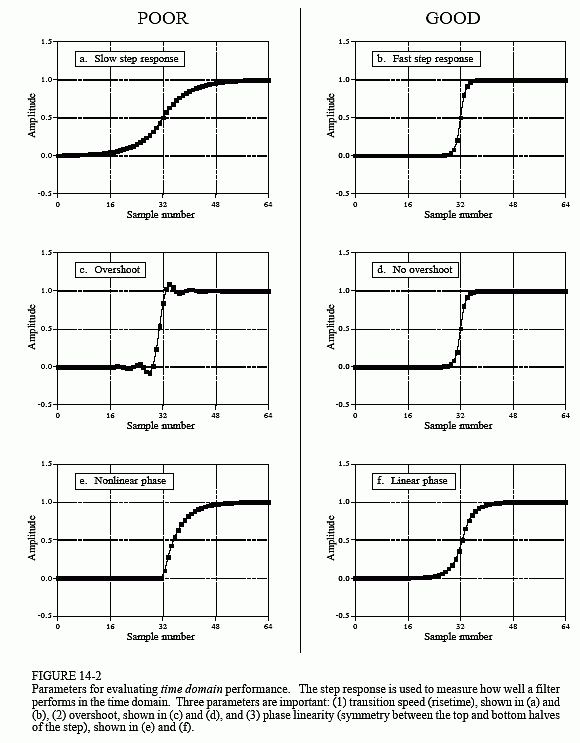
Figures (c) and (d) shows the next parameter that is important: overshoot in the step response. Overshoot must generally be eliminated because it changes the amplitude of samples in the signal; this is a basic distortion of the information contained in the time domain. This can be summed up in
one question: Is the overshoot you observe in a signal coming from the thing you are trying to measure, or from the filter you have used?
Finally, it is often desired that the upper half of the step response be symmetrical with the lower half, as illustrated in (e) and (f). This symmetry is needed to make the rising edges look the same as the falling edges. This symmetry is called linear phase, because the frequency response has a phase that is a straight line (discussed in Chapter 19). Make sure you understand these three parameters; they are the key to evaluating time domain filters.
