The Scientist and Engineer's Guide to
Digital Signal Processing
By Steven W. Smith, Ph.D.
Book Search
Table of contents
- 1: The Breadth and Depth of DSP
- 2: Statistics, Probability and Noise
- 3: ADC and DAC
- 4: DSP Software
- 5: Linear Systems
- 6: Convolution
- 7: Properties of Convolution
- 8: The Discrete Fourier Transform
- 9: Applications of the DFT
- 10: Fourier Transform Properties
- 11: Fourier Transform Pairs
- 12: The Fast Fourier Transform
- 13: Continuous Signal Processing
- 14: Introduction to Digital Filters
- 15: Moving Average Filters
- 16: Windowed-Sinc Filters
- 17: Custom Filters
- 18: FFT Convolution
- 19: Recursive Filters
- 20: Chebyshev Filters
- 21: Filter Comparison
- 22: Audio Processing
- 23: Image Formation & Display
- 24: Linear Image Processing
- 25: Special Imaging Techniques
- 26: Neural Networks (and more!)
- 27: Data Compression
- 28: Digital Signal Processors
- 29: Getting Started with DSPs
- 30: Complex Numbers
- 31: The Complex Fourier Transform
- 32: The Laplace Transform
- 33: The z-Transform
- 34: Explaining Benford's Law
How to order your own hardcover copy
Wouldn't you rather have a bound book instead of 640 loose pages?Your laser printer will thank you!
Order from Amazon.com.
Chapter 34: Explaining Benford's Law
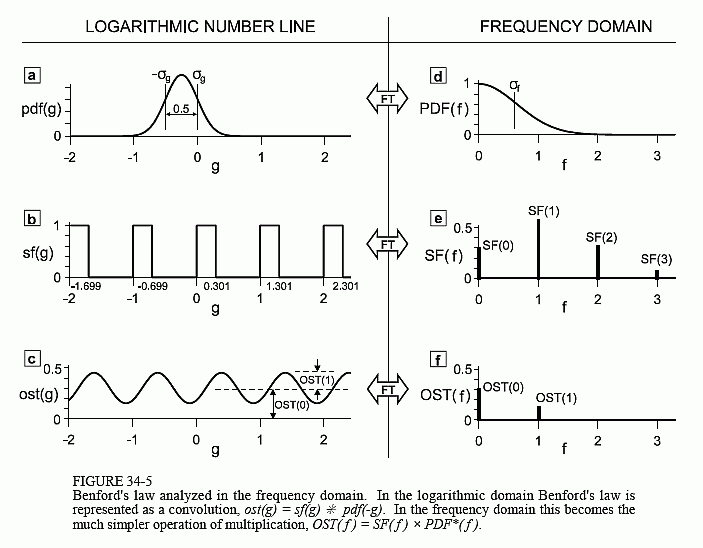
Figure 34-5 is what we have been working toward, a systematic way of understanding the operation of Benford's law. The left three signals, the logarithmic domain, are pdf(g), sf(g) and ost(g). The particular examples in this figure are the same ones we used previously (i.e., Fig. 34-4). These three signals are related by convolution (Eq. 34-3), a mathematical operation that is not especially easy to deal with. To overcome this we move the problem into the frequency domain by taking the Fourier transform of each signal. Using standard DSP notation, we will represent the Fourier transforms of pdf(g), sf(g), and ost(g), as PDF(f), SF(f), and OST(f), respectively. These are shown on the right side of Fig. 34-5.
By moving the problem into the frequency domain we replace the difficult operation of convolution with the simple operation of multiplication. That is, the six signals in Fig. 34-5 are related as follows:
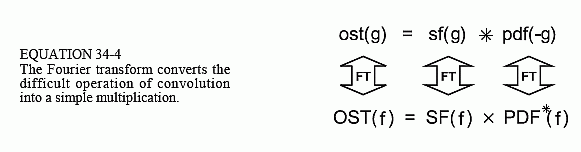
A small detail: The Fourier transform of pdf(g) is PDF(f), while the Fourier transform of pdf(-g) is PDF*(f). The star in PDF*(f) means it is the complex conjugate of PDF(f), indicating that all of the phase values are changed in sign. However, notice that Fig. 34-5 only shows the magnitudes; we are completely ignoring the phases. The reason for this is simple– the phase does not contain information we are interested in for this particular problem. This makes it unimportant if we use pdf(g) vs. pdf(-g), or PDF(f) vs. PDF*(f).
Notice how these signals represent the key components of Benford's law. First, there is a group of numbers or a probability density function that can generate a group of numbers. This is represented by pdf(g) and PDF(f). Second, we modify each number in this group or distribution by taking its leading digit. This action is represented by convolving pdf(g) with sf(g), or by multiplying PDF(f) by SF(f). Third, we observe that the leading digits often have an unusual property. This unusual characteristic is seen in ost(g) and OST(f).
All six of these signals have specific characteristics that are fixed by the definition of the problem. For instance, the value at f=0 in the frequency domain always corresponds to the average value of the signal in the logarithmic domain. In particular, this means that PDF(0) will always be equal to one, since the area under pdf(g) is unity. In this example we are using a Gaussian curve for pdf(g). One of the interesting properties of the Gaussian is that its Fourier Transform is also a Gaussian, one-sided in this case, as shown in Fig. (d). These are related by σf = 1/(2πσg).
Since sf(g) is periodic with a period of one, SF(f) consists of a series of spikes at f = 0, 1, 2, 3, ..., with all other values being zero. This is a standard transform pair, given by Fig. 13-10 in chapter 13. The zeroth spike, SF(0), is the average value of sf(g). This is equal to the fraction of the time that the signal is in the high state, or log(2) - log(1) = 0.301. The remaining spikes have amplitudes: SF(1) = 0.516, SF(2) = 0.302, SF(3) = 0.064, and so on, as calculated from the above reference.
Lastly we come to ost(g) and OST(f). If Benford's law is being followed, ost(g) will be a flat line with a value of 0.301. This corresponds to OST(0) = 0.301, with all other values in OST(f) being zero. However, if Benford's law is not being followed, then ost(g) will be periodic with a period of one, as show in Fig. (c). Therefore, OST(f) will be a series of spikes at f = 0, 1, 2, 3, ..., with the space between being zero.
