The Scientist and Engineer's Guide to
Digital Signal Processing
By Steven W. Smith, Ph.D.
Book Search
Table of contents
- 1: The Breadth and Depth of DSP
- 2: Statistics, Probability and Noise
- 3: ADC and DAC
- 4: DSP Software
- 5: Linear Systems
- 6: Convolution
- 7: Properties of Convolution
- 8: The Discrete Fourier Transform
- 9: Applications of the DFT
- 10: Fourier Transform Properties
- 11: Fourier Transform Pairs
- 12: The Fast Fourier Transform
- 13: Continuous Signal Processing
- 14: Introduction to Digital Filters
- 15: Moving Average Filters
- 16: Windowed-Sinc Filters
- 17: Custom Filters
- 18: FFT Convolution
- 19: Recursive Filters
- 20: Chebyshev Filters
- 21: Filter Comparison
- 22: Audio Processing
- 23: Image Formation & Display
- 24: Linear Image Processing
- 25: Special Imaging Techniques
- 26: Neural Networks (and more!)
- 27: Data Compression
- 28: Digital Signal Processors
- 29: Getting Started with DSPs
- 30: Complex Numbers
- 31: The Complex Fourier Transform
- 32: The Laplace Transform
- 33: The z-Transform
- 34: Explaining Benford's Law
How to order your own hardcover copy
Wouldn't you rather have a bound book instead of 640 loose pages?Your laser printer will thank you!
Order from Amazon.com.
Chapter 29: Getting Started with DSPs
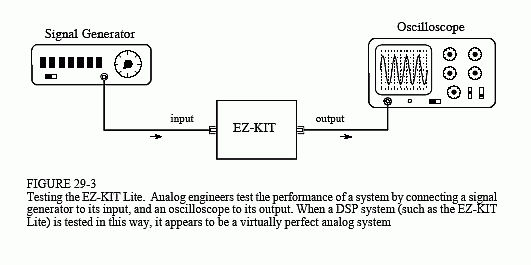
For just a few moments, forget that you are studying digital techniques. Let's take a look at this from the standpoint of an engineer that specializes in analog electronics. He doesn't care what is inside of the EZ-KIT Lite, only that it has an analog input and an analog output. As shown in Fig. 29-3, he would invoke the traditional analog method of analyzing a "black box," attach a signal generator to the input, and look at the output on an oscilloscope.
What does our analog guru find? First, the system is linear (as least as far as this simple test can tell). If a sine wave is placed into the input, a sine wave is observed on the output. If the amplitude or frequency of the input is changed, a corresponding change is seen in the output. When the input frequency is slowly increased, there comes a point where the amplitude of the output sine wave decreases rapidly to zero. That occurs just below one-half the sampling rate, due to the action of the anti-alias filter on the ADC.
Now our engineer notices something unknown in the analog world: the system has a perfect linear phase. In other words, there is a constant delay between an event occurring in the input signal, and the result of that event in the output signal. For instance, consider our example filter kernel in Fig. 29-3. Since the center of symmetry is at sample 150, the output signal will be delayed by 150 samples relative to the input signal. If the system is sampling at 8 kHz, for example, this delay will be 18.75 milliseconds. In addition, the sigma-delta converter will also provide a small additional fixed delay.
Our analog engineer will become very agitated when he sees this linear phase. The signals won't appear the way he thinks they should, and he will start twisting knobs at lightning speed. He will complain that the triggering isn't working right, and mumble such things as: "this doesn't make sense," what's going on here?", and "who's been playing with my oscilloscope?" The performance of DSP systems is so good, it will take him a few minutes before he understands what he is seeing.
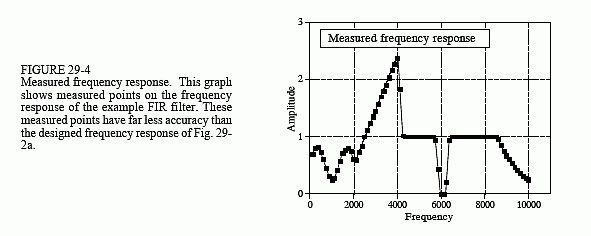
To make him even more impressed, we ask our engineer to manually measure the frequency response of the system. To do this, he will step the signal generator through all the frequencies between 125 Hz and 10 kHz in increments of 125 Hz. At each frequency he measures the amplitude of the output signal and divides it by the amplitude of the input signal. (Of course, the easiest way to do this is to keep the input signal at a constant amplitude). We set the sampling rate of the EZ-KIT Lite at 22 kHz for this test. In other words, the 0 to 0.5 digital frequency of Fig. 29-2a is mapped to DC to 11 kHz in our real world measurement.
Figure 29-4 shows actual measurements taken on the EZ-KIT Lite; it couldn't be better! The measured data points agree with the theoretical curve within the limit of measurement error. This is something our analog engineer has never seen with filters made from resistors, capacitors, and inductors.
However, even this doesn't give the DSP the credit it deserves. Analog measurements using oscilloscopes and digital-volt-meters have a typical accuracy and precision of about 0.1% to 1%. In comparison, this DSP system is limited only by the â ˜0.001% round-off error of the 16 bit codec, since the internal calculations use floating point. In other words, the device being evaluated is one-hundred times more precise than the measurement tool being used. A proper evaluation of the frequency response would require a specialized instrument, such as a computerized data acquisition system with a 20 bit ADC. Given these facts, it is not surprising that DSPs are often used in measurement instruments to achieve high precision.
Now we can answer the question: Why does Analog Devices sell Digital Signal Processors? Only a decade ago, state-of-the-art signal processing was carried out with precision op amps and similar transistor circuits. Today, the highest quality analog processing is accomplished with digital techniques. Analog Devices is a great role-model for individuals and other companies; hold on to your vision and goals, but don't be afraid to adapt with the changing technology!
