The Scientist and Engineer's Guide to
Digital Signal Processing
By Steven W. Smith, Ph.D.
Book Search
Table of contents
- 1: The Breadth and Depth of DSP
- 2: Statistics, Probability and Noise
- 3: ADC and DAC
- 4: DSP Software
- 5: Linear Systems
- 6: Convolution
- 7: Properties of Convolution
- 8: The Discrete Fourier Transform
- 9: Applications of the DFT
- 10: Fourier Transform Properties
- 11: Fourier Transform Pairs
- 12: The Fast Fourier Transform
- 13: Continuous Signal Processing
- 14: Introduction to Digital Filters
- 15: Moving Average Filters
- 16: Windowed-Sinc Filters
- 17: Custom Filters
- 18: FFT Convolution
- 19: Recursive Filters
- 20: Chebyshev Filters
- 21: Filter Comparison
- 22: Audio Processing
- 23: Image Formation & Display
- 24: Linear Image Processing
- 25: Special Imaging Techniques
- 26: Neural Networks (and more!)
- 27: Data Compression
- 28: Digital Signal Processors
- 29: Getting Started with DSPs
- 30: Complex Numbers
- 31: The Complex Fourier Transform
- 32: The Laplace Transform
- 33: The z-Transform
- 34: Explaining Benford's Law
How to order your own hardcover copy
Wouldn't you rather have a bound book instead of 640 loose pages?Your laser printer will thank you!
Order from Amazon.com.
Chapter 10: Fourier Transform Properties
Unlike the other three Fourier Transforms, the DFT views both the time domain and the frequency domain as periodic. This can be confusing and inconvenient since most of the signals used in DSP are not periodic. Nevertheless, if you want to use the DFT, you must conform with the DFT's view of the world.
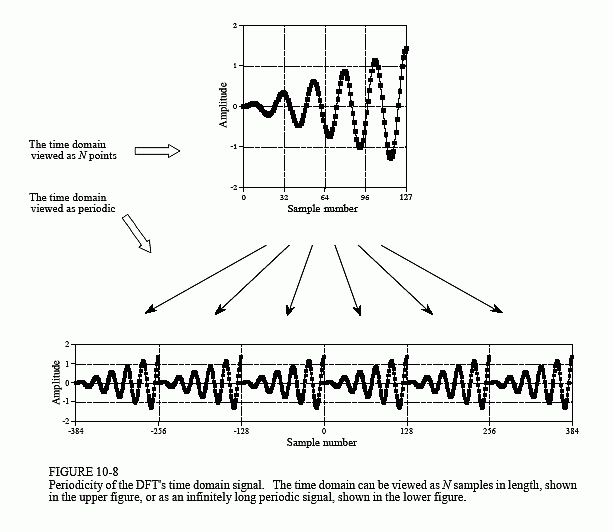
Figure 10-8 shows two different interpretations of the time domain signal. First, look at the upper signal, the time domain viewed as N points. This represents how digital signals are typically acquired in scientific experiments and engineering applications. For instance, these 128 samples might have been acquired by sampling some parameter at regular intervals of time. Sample 0 is distinct and separate from sample 127 because they were acquired at different times. From the way this signal was formed, there is no reason to think that the samples on the left of the signal are even related to the samples on the right.
Unfortunately, the DFT doesn't see things this way. As shown in the lower figure, the DFT views these 128 points to be a single period of an infinitely long periodic signal. This means that the left side of the acquired signal is connected to the right side of a duplicate signal. Likewise, the right side of the acquired signal is connected to the left side of an identical period. This can also be thought of as the right side of the acquired signal wrapping around and connecting to its left side. In this view, sample 127 occurs next to sample 0, just as sample 43 occurs next to sample 44. This is referred to as being circular, and is identical to viewing the signal as being periodic.
The most serious consequence of this periodicity is time domain aliasing. To illustrate this, suppose we take a time domain signal and pass it through the DFT to find its frequency spectrum. We could immediately pass this frequency spectrum through an Inverse DFT to reconstruct the original time domain signal, but the entire procedure wouldn't be very interesting. Instead, we will modify the frequency spectrum in some manner before using the Inverse DFT. For instance, selected frequencies might be deleted, changed in amplitude or phase, shifted around, etc. These are the kinds of things routinely done in DSP. Unfortunately, these changes in the frequency domain can create a time domain signal that is too long to fit into
a single period. This forces the signal to spill over from one period into the adjacent periods. When the time domain is viewed as circular, portions of the signal that overflow on the right suddenly seem to reappear on the left side of the signal, and vice versa. That is, the overflowing portions of the signal alias themselves to a new location in the time domain. If this new location happens to already contain an existing signal, the whole mess adds, resulting in a loss of information. Circular convolution resulting from frequency domain multiplication (discussed in Chapter 9), is an excellent example of this type of aliasing.
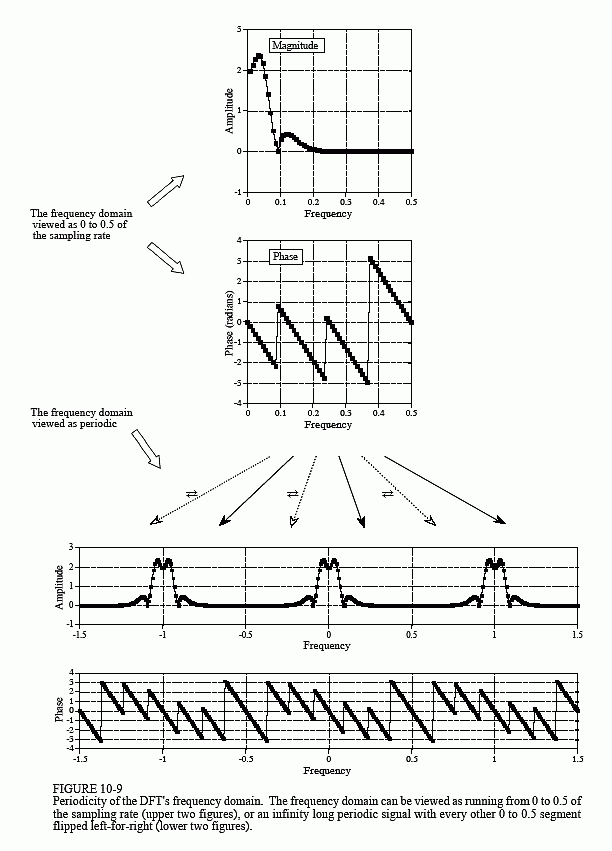
Periodicity in the frequency domain behaves in much the same way, but is more complicated. Figure 10-9 shows an example. The upper figures show the magnitude and phase of the frequency spectrum, viewed as being composed of N/2 + 1 samples spread between 0 and 0.5 of the sampling rate. This is the simplest way of viewing the frequency spectrum, but it doesn't explain many of the DFT's properties.
The lower two figures show how the DFT views this frequency spectrum as being periodic. The key feature is that the frequency spectrum between 0 and 0.5 appears to have a mirror image of frequencies that run between 0 and -0.5. This mirror image of negative frequencies is slightly different for the magnitude and the phase signals. In the magnitude, the signal is flipped left-for-right. In the phase, the signal is flipped left-for-right, and changed in sign. As you recall, these two types of symmetry are given names: the magnitude is said to be an even signal (it has even symmetry), while the phase is said to be an odd signal (it has odd symmetry). If the frequency spectrum is converted into the real and imaginary parts, the real part will always be even, while the imaginary part will always be odd.
Taking these negative frequencies into account, the DFT views the frequency domain as periodic, with a period of 1.0 times the sampling rate, such as -0.5 to 0.5, or 0 to 1.0. In terms of sample numbers, this makes the length of the frequency domain period equal to N, the same as in the time domain.
The periodicity of the frequency domain makes it susceptible to frequency domain aliasing, completely analogous to the previously described time domain aliasing. Imagine a time domain signal that corresponds to some frequency spectrum. If the time domain signal is modified, it is obvious that the frequency spectrum will also be changed. If the modified frequency spectrum cannot fit in the space provided, it will push into the adjacent periods. Just as before, this aliasing causes two problems: frequencies aren't where they should be, and overlapping frequencies from different periods add, destroying information.
Frequency domain aliasing is more difficult to understand than time domain aliasing, since the periodic pattern is more complicated in the frequency domain. Consider a single frequency that is being forced to move from 0.01 to 0.49 in the frequency domain. The corresponding negative frequency is therefore moving from -0.01 to -0.49. When the positive frequency moves
across the 0.5 barrier, the negative frequency is pushed across the -0.5 barrier. Since the frequency domain is periodic, these same events are occurring in the other periods, such as between 0.5 and 1.5. A clone of the positive frequency is crossing frequency 1.5 from left to right, while a clone of the negative frequency is crossing 0.5 from right to left. Now imagine what this looks like if you can only see the frequency band of 0 to 0.5. It appears that a frequency leaving to the right, reappears on the right, but moving in the opposite direction.
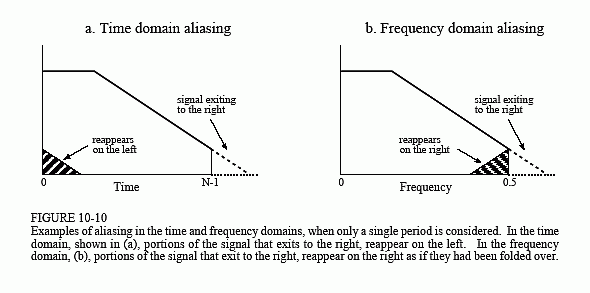
Figure 10-10 illustrates how aliasing appears in the time and frequency domains when only a single period is viewed. As shown in (a), if one end of a time domain signal is too long to fit inside a single period, the protruding end will be cut off and pasted onto the other side. In comparison, (b) shows that when a frequency domain signal overflows the period, the protruding end is folded over. Regardless of where the aliased segment ends up, it adds to whatever signal is already there, destroying information.
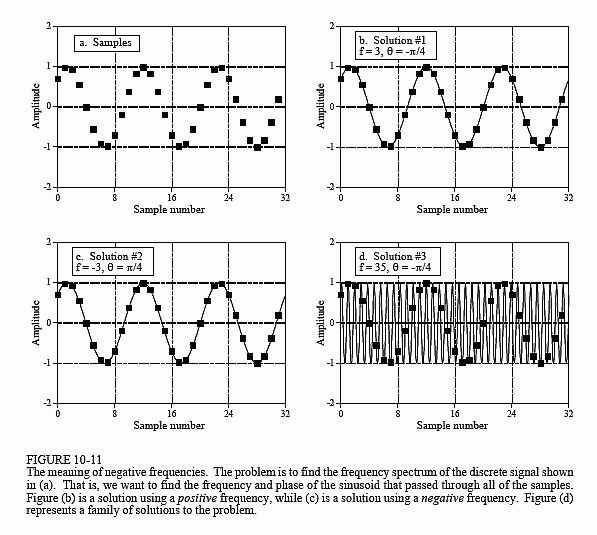
Let's take a closer look at these strange things called negative frequencies. Are they just some bizarre artifact of the mathematics, or do they have a real world meaning? Figure 10-11 shows what they are about. Figure (a) is a discrete signal composed of 32 samples. Imagine that you are given the task of finding the frequency spectrum that corresponds to these 32 points. To make your job easier, you are told that these points represent a discrete cosine wave. In other words, you must find the frequency and phase shift (f and θ) such that x[n] = cos(2πnf/N + θ) matches the given samples. It isn't long before you come up with the solution shown in (b), that is, f = 3 and θ = -π/4.
If you stopped your analysis at this point, you only get 1/3 credit for the problem. This is because there are two other solutions that you have missed. As shown in (c), the second solution is f = -3 and θ = π/4. Even if the idea of a negative frequency offends your sensibilities, it doesn't
change the fact that it is a mathematically valid solution to the defined problem. Every positive frequency sinusoid can alternately be expressed as a negative frequency sinusoid. This applies to continuous as well as discrete signals.
The third solution is not a single answer, but an infinite family of solutions. As shown in (d), the sinusoid with f = 35 and θ = -π/4 passes through all of the discrete points, and is therefore a correct solution. The fact that it shows oscillation between the samples may be confusing, but it doesn't disqualify it from being an authentic answer. Likewise, f = ±29, f = ?35, f = ?61, and f = ?67 are all solutions with multiple oscillations between the points. This third group of solutions requires the original signal to be discrete, rather than continuous. With continuous signals, you can't have oscillations between the samples, because you don't have samples.
Each of these three solutions corresponds to a different section of the frequency spectrum. For discrete signals, the first solution corresponds to frequencies between 0 and 0.5 of the sampling rate. The second solution results in frequencies between 0 and -0.5. Lastly, the third solution makes up the infinite number of duplicated frequencies below -0.5 and above 0.5. With continuous signals, the first solution results in frequencies from zero to positive infinity, while the second solution results in frequencies from zero to negative infinity.
Many DSP techniques do not require the use of negative frequencies, or an understanding of the DFT's periodicity. For example, two common ones were described in the last chapter, spectral analysis, and the frequency response of systems. For these applications, it is completely sufficient to view the time domain as extending from sample 0 to N-1, and the frequency domain from zero to one-half of the sampling frequency. These techniques can use a simpler view of the world because they never result in portions of one period moving into another period. With this restriction, looking at a single period is no different from looking at the entire periodic signal.
However, certain procedures can only be analyzed by considering how signals overflow between periods. Two examples of this have already been presented, circular convolution and analog-to-digital conversion. In circular convolution, multiplication of the frequency spectra results in the time domain signals being convolved. If the resulting time domain signal is too long to fit inside a single period, it overflows into the adjacent periods, resulting in time domain aliasing. In contrast, analog-to-digital conversion is an example of frequency domain aliasing. A nonlinear action is taken in the time domain, that is, changing a continuous signal into a discrete signal by sampling. The problem is, the spectrum of the original analog signal may be too long to fit inside the discrete signal's spectrum. When we force the situation, the ends of the spectrum protrude into adjacent periods. Let's look at two more examples where the periodic nature of the DFT is important, compression & expansion of signals, and amplitude modulation.
