The Scientist and Engineer's Guide to
Digital Signal Processing
By Steven W. Smith, Ph.D.
Book Search
Table of contents
- 1: The Breadth and Depth of DSP
- 2: Statistics, Probability and Noise
- 3: ADC and DAC
- 4: DSP Software
- 5: Linear Systems
- 6: Convolution
- 7: Properties of Convolution
- 8: The Discrete Fourier Transform
- 9: Applications of the DFT
- 10: Fourier Transform Properties
- 11: Fourier Transform Pairs
- 12: The Fast Fourier Transform
- 13: Continuous Signal Processing
- 14: Introduction to Digital Filters
- 15: Moving Average Filters
- 16: Windowed-Sinc Filters
- 17: Custom Filters
- 18: FFT Convolution
- 19: Recursive Filters
- 20: Chebyshev Filters
- 21: Filter Comparison
- 22: Audio Processing
- 23: Image Formation & Display
- 24: Linear Image Processing
- 25: Special Imaging Techniques
- 26: Neural Networks (and more!)
- 27: Data Compression
- 28: Digital Signal Processors
- 29: Getting Started with DSPs
- 30: Complex Numbers
- 31: The Complex Fourier Transform
- 32: The Laplace Transform
- 33: The z-Transform
- 34: Explaining Benford's Law
How to order your own hardcover copy
Wouldn't you rather have a bound book instead of 640 loose pages?Your laser printer will thank you!
Order from Amazon.com.
Chapter 34: Explaining Benford's Law
Given a set of numbers, the simplest test for Benford's law is to count how many of the numbers have 1 as the leading digit. This fraction will be about 0.301 if Benford's law is being followed. However, even finding this value exactly is not sufficient to conclude that the numbers are obeying the law. For instance, the set might have 30.1% of the numbers with a value of 1.00, and 69.9% with a value of 2.00. We can overcome this problem by including a test for scale invariance. That is, we multiply each number in the set by some constant, and then recounting how many numbers have 1 as their leading digit. If Benford's law is truly being followed, the percentage of numbers beginning with the digit 1 will remain about 30.1%, regardless of the constant we use.
A computer program can make this procedure more systematic, such as the example in Table 34-1. This program loops through the evaluation 696 times, with each loop multiplying all numbers in the group by 1.01. On the first loop each of the original numbers will be multiplied by 1.01. On the second loop each number will be multiplied by 1.01 again, in addition to the multiplication that took place on the first loop. By the time we reach the 80th loop, each number will have been multiplied by 1.01 a total of 80 times. Therefore, the numbers on the 80th loop are the same as multiplying each of the original numbers by 1.0180, or 2.217. At the completion of the program the numbers will have been multiplied 696 times, equivalent to multiplying the original numbers by a constant of 1.01696 ≈ 1,000. In other words, this computer program systematically scales the data in small increments over about three orders of magnitude.
The fraction of numbers having 1 as the leading digit is tallied on each of these 696 steps and stored in an array, which we will call the Ones Scaling Test. Figure 34-3 shows the values in this array for the two
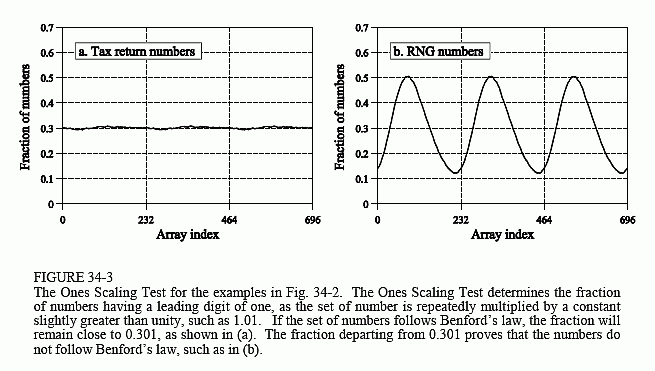
examples in Fig. 34-2. As expected, the Ones Scaling Test for the income tax numbers is a relatively constant value around 30.1%, proving that it follows Benford's law very closely. As also expected, the Ones Scaling Test for the random number generator shows wild fluctuations, as high as 51% and as low as 12%.
An important point to notice in Fig. 34-3 is that the Ones Scaling Test is periodic, repeating itself when the multiplication constant reaches a factor of ten. In this example the period is 232 entries in the array, since 1.01232 ≈ 10. Say you start with the number 3.12345 and multiply it by 10 to get 31.2345. These two numbers, 3.12345 and 31.2345, are exactly the same when you are only concerned with the leading digit, and the entire pattern repeats.
Pay particular attention to the operations in lines 400 to 430 of Table 34- 1. This is where the program determines the leading digit of the number being evaluated. In line 310, one of the 10,000 numbers being tested is transferred to the variable: TESTX. The leading digit of TESTX, eventually held in the variable LD, is calculated in four steps. In line 400 we eliminate the sign of the number by taking the absolute value. Lines 410 and 420 repeatedly multiply or divide the number by a factor a ten, as needed, until the number is between 1 and 9.999999. For instance, line 410 tests the number for being less than 1. If it is, the number is multiplied by 10, and the line is repeated. When the number finally exceeds 1, the program moves to the next line. In line 430 we extract the integer portion of the number, which is the leading digit. Make sure you understand these steps; they are key to understanding what is really going on in Benford's law.
