The Scientist and Engineer's Guide to
Digital Signal Processing
By Steven W. Smith, Ph.D.
Book Search
Table of contents
- 1: The Breadth and Depth of DSP
- 2: Statistics, Probability and Noise
- 3: ADC and DAC
- 4: DSP Software
- 5: Linear Systems
- 6: Convolution
- 7: Properties of Convolution
- 8: The Discrete Fourier Transform
- 9: Applications of the DFT
- 10: Fourier Transform Properties
- 11: Fourier Transform Pairs
- 12: The Fast Fourier Transform
- 13: Continuous Signal Processing
- 14: Introduction to Digital Filters
- 15: Moving Average Filters
- 16: Windowed-Sinc Filters
- 17: Custom Filters
- 18: FFT Convolution
- 19: Recursive Filters
- 20: Chebyshev Filters
- 21: Filter Comparison
- 22: Audio Processing
- 23: Image Formation & Display
- 24: Linear Image Processing
- 25: Special Imaging Techniques
- 26: Neural Networks (and more!)
- 27: Data Compression
- 28: Digital Signal Processors
- 29: Getting Started with DSPs
- 30: Complex Numbers
- 31: The Complex Fourier Transform
- 32: The Laplace Transform
- 33: The z-Transform
- 34: Explaining Benford's Law
How to order your own hardcover copy
Wouldn't you rather have a bound book instead of 640 loose pages?Your laser printer will thank you!
Order from Amazon.com.
Chapter 7: Properties of Convolution
The concept of correlation can best be presented with an example. Figure 7-13 shows the key elements of a radar system. A specially designed antenna transmits a short burst of radio wave energy in a selected direction. If the propagating wave strikes an object, such as the helicopter in this illustration, a small fraction of the energy is reflected back toward a radio receiver located near the transmitter. The transmitted pulse is a specific shape that we have selected, such as the triangle shown in this example. The received signal will consist of two parts: (1) a shifted and scaled version of the transmitted pulse, and (2) random noise, resulting from interfering radio waves, thermal noise in the electronics, etc. Since radio signals travel at a known rate, the speed of light, the shift between the transmitted and received pulse is a direct measure of the distance to the object being detected. This is the problem: given a signal of some known shape, what is the best way to determine where (or if) the signal occurs in another signal. Correlation is the answer.
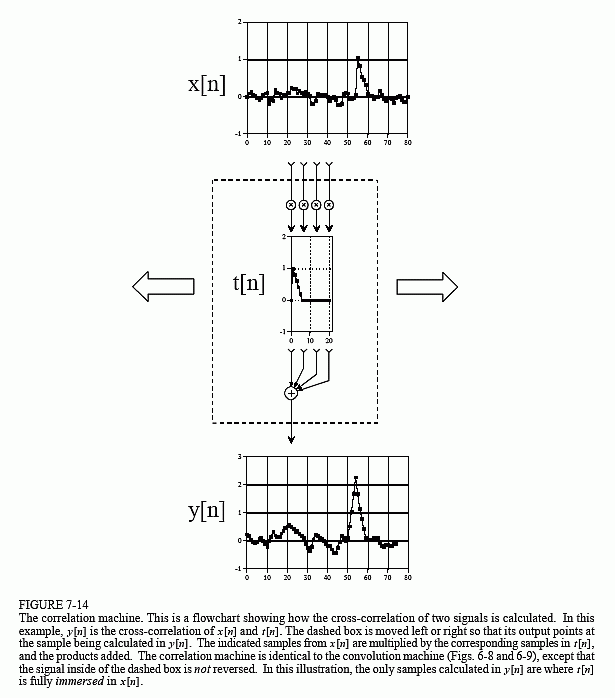
Correlation is a mathematical operation that is very similar to convolution. Just as with convolution, correlation uses two signals to produce a third signal. This third signal is called the cross-correlation of the two input signals. If a signal is correlated with itself, the resulting signal is instead called the autocorrelation. The convolution machine was presented in the last chapter to show how convolution is performed. Figure 7-14 is a similar
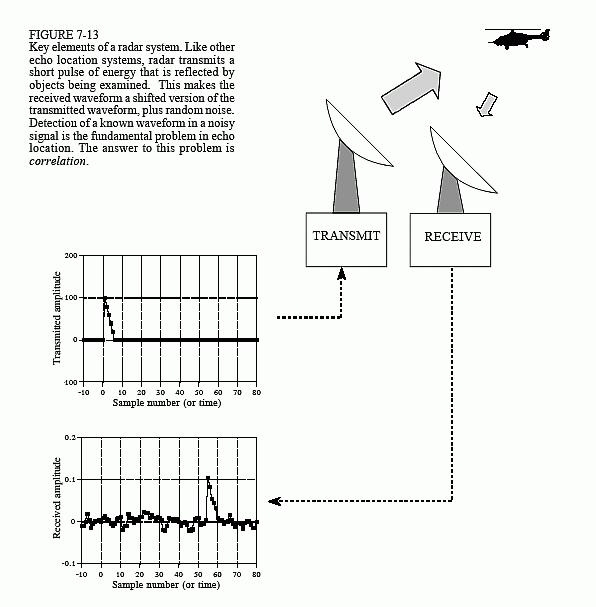
illustration of a correlation machine. The received signal, x[n], and the cross-correlation signal, y[n], are fixed on the page. The waveform we are looking for, t[n], commonly called the target signal, is contained within the correlation machine. Each sample in y[n] is calculated by moving the correlation machine left or right until it points to the sample being worked on. Next, the indicated samples from the received signal fall into the correlation machine, and are multiplied by the corresponding points in the target signal. The sum of these products then moves into the proper sample in the cross-correlation signal.
The amplitude of each sample in the cross-correlation signal is a measure of how much the received signal resembles the target signal, at that location. This means that a peak will occur in the cross-correlation signal for every target signal that is present in the received signal. In other words, the value of the cross-correlation is maximized when the target signal is aligned with the same features in the received signal.
What if the target signal contains samples with a negative value? Nothing changes. Imagine that the correlation machine is positioned such that the target signal is perfectly aligned with the matching waveform in the received signal. As samples from the received signal fall into the correlation machine, they are multiplied by their matching samples in the target signal. Neglecting noise, a positive sample will be multiplied by itself, resulting in a positive number. Likewise, a negative sample will be multiplied by itself, also resulting in a positive number. Even if the target signal is completely negative, the peak in the cross-correlation will still be positive.
If there is noise on the received signal, there will also be noise on the cross-correlation signal. It is an unavoidable fact that random noise looks a certain amount like any target signal you can choose. The noise on the cross-correlation signal is simply measuring this similarity. Except for this noise, the peak generated in the cross-correlation signal is symmetrical between its left and right. This is true even if the target signal isn't symmetrical. In addition, the width of the peak is twice the width of the target signal. Remember, the cross-correlation is trying to detect the target signal, not recreate it. There is no reason to expect that the peak will even look like the target signal.
Correlation is the optimal technique for detecting a known waveform in random noise. That is, the peak is higher above the noise using correlation than can be produced by any other linear system. (To be perfectly correct, it is only optimal for random white noise). Using correlation to detect a known waveform is frequently called matched filtering. More on this in Chapter 17.
The correlation machine and convolution machine are identical, except for one small difference. As discussed in the last chapter, the signal inside of the convolution machine is flipped left-for-right. This means that samples numbers: 1, 2, 3 … run from the right to the left. In the correlation machine this flip doesn't take place, and the samples run in the normal direction.
Since this signal reversal is the only difference between the two operations, it is possible to represent correlation using the same mathematics as convolution. This requires preflipping one of the two signals being correlated, so that the left-for-right flip inherent in convolution is canceled. For instance, when a[n] and b[n], are convolved to produce c[n], the equation is written: a[n] * b[n] = c[n]. In comparison, the cross-correlation of a[n] and b[n] can be written: a[n] * b[-n] = c[n]. That is, flipping b[n] left-for-right is accomplished by reversing the sign of the index, i.e., b[-n].
Don't let the mathematical similarity between convolution and correlation fool you; they represent very different DSP procedures. Convolution is the relationship between a system's input signal, output signal, and impulse response. Correlation is a way to detect a known waveform in a noisy background. The similar mathematics is only a convenient coincidence.
