The Scientist and Engineer's Guide to
Digital Signal Processing
By Steven W. Smith, Ph.D.
Book Search
Table of contents
- 1: The Breadth and Depth of DSP
- 2: Statistics, Probability and Noise
- 3: ADC and DAC
- 4: DSP Software
- 5: Linear Systems
- 6: Convolution
- 7: Properties of Convolution
- 8: The Discrete Fourier Transform
- 9: Applications of the DFT
- 10: Fourier Transform Properties
- 11: Fourier Transform Pairs
- 12: The Fast Fourier Transform
- 13: Continuous Signal Processing
- 14: Introduction to Digital Filters
- 15: Moving Average Filters
- 16: Windowed-Sinc Filters
- 17: Custom Filters
- 18: FFT Convolution
- 19: Recursive Filters
- 20: Chebyshev Filters
- 21: Filter Comparison
- 22: Audio Processing
- 23: Image Formation & Display
- 24: Linear Image Processing
- 25: Special Imaging Techniques
- 26: Neural Networks (and more!)
- 27: Data Compression
- 28: Digital Signal Processors
- 29: Getting Started with DSPs
- 30: Complex Numbers
- 31: The Complex Fourier Transform
- 32: The Laplace Transform
- 33: The z-Transform
- 34: Explaining Benford's Law
How to order your own hardcover copy
Wouldn't you rather have a bound book instead of 640 loose pages?Your laser printer will thank you!
Order from Amazon.com.
Chapter 2: Statistics, Probability and Noise
Precision and accuracy are terms used to describe systems and methods that measure, estimate, or predict. In all these cases, there is some parameter you wish to know the value of. This is called the true value, or simply, truth. The method provides a measured value, that you want to be as close to the true value as possible. Precision and accuracy are ways of describing the error that can exist between these two values.
Unfortunately, precision and accuracy are used interchangeably in non-technical settings. In fact, dictionaries define them by referring to each other! In spite of this, science and engineering have very specific definitions for each. You should make a point of using the terms correctly, and quietly tolerate others when they use them incorrectly.
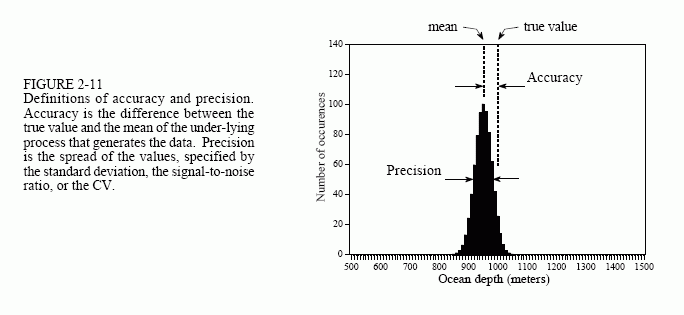
As an example, consider an oceanographer measuring water depth using a sonar system. Short bursts of sound are transmitted from the ship, reflected from the ocean floor, and received at the surface as an echo. Sound waves travel at a relatively constant velocity in water, allowing the depth to be found from the elapsed time between the transmitted and received pulses. As with all empirical measurements, a certain amount of error exists between the measured and true values. This particular measurement could be affected by many factors: random noise in the electronics, waves on the ocean surface, plant growth on the ocean floor, variations in the water temperature causing the sound velocity to change, etc.
To investigate these effects, the oceanographer takes many successive readings at a location known to be exactly 1000 meters deep (the true value). These measurements are then arranged as the histogram shown in Fig. 2-11. As would be expected from the Central Limit Theorem, the acquired data are normally distributed. The mean occurs at the center of the distribution, and represents the best estimate of the depth based on all of the measured data. The standard deviation defines the width of the distribution, describing how much variation occurs between successive measurements.
This situation results in two general types of error that the system can experience. First, the mean may be shifted from the true value. The amount of this shift is called the accuracy of the measurement. Second, individual measurements may not agree well with each other, as indicated by the width of the distribution. This is called the precision of the measurement, and is expressed by quoting the standard deviation, the signal-to-noise ratio, or the CV.
Consider a measurement that has good accuracy, but poor precision; the histogram is centered over the true value, but is very broad. Although the measurements are correct as a group, each individual reading is a poor measure of the true value. This situation is said to have poor repeatability; measurements taken in succession don't agree well. Poor precision results from random errors. This is the name given to errors that change each
time the measurement is repeated. Averaging several measurements will always improve the precision. In short, precision is a measure of random noise.
Now, imagine a measurement that is very precise, but has poor accuracy. This makes the histogram very slender, but not centered over the true value. Successive readings are close in value; however, they all have a large error. Poor accuracy results from systematic errors. These are errors that become repeated in exactly the same manner each time the measurement is conducted. Accuracy is usually dependent on how you calibrate the system. For example, in the ocean depth measurement, the parameter directly measured is elapsed time. This is converted into depth by a calibration procedure that relates milliseconds to meters. This may be as simple as multiplying by a fixed velocity, or as complicated as dozens of second order corrections. Averaging individual measurements does nothing to improve the accuracy. In short, accuracy is a measure of calibration.
In actual practice there are many ways that precision and accuracy can become intertwined. For example, imagine building an electronic amplifier from 1% resistors. This tolerance indicates that the value of each resistor will be within 1% of the stated value over a wide range of conditions, such as temperature, humidity, age, etc. This error in the resistance will produce a corresponding error in the gain of the amplifier. Is this error a problem of accuracy or precision?
The answer depends on how you take the measurements. For example, suppose you build one amplifier and test it several times over a few minutes. The error in gain remains constant with each test, and you conclude the problem is accuracy. In comparison, suppose you build one thousand of the amplifiers. The gain from device to device will fluctuate randomly, and the problem appears to be one of precision. Likewise, any one of these amplifiers will show gain fluctuations in response to temperature and other environmental changes. Again, the problem would be called precision.
When deciding which name to call the problem, ask yourself two questions. First: Will averaging successive readings provide a better measurement? If yes, call the error precision; if no, call it accuracy. Second: Will calibration correct the error? If yes, call it accuracy; if no, call it precision. This may require some thought, especially related to how the device will be calibrated, and how often it will be done.
