The Scientist and Engineer's Guide to
Digital Signal Processing
By Steven W. Smith, Ph.D.
Book Search
Table of contents
- 1: The Breadth and Depth of DSP
- 2: Statistics, Probability and Noise
- 3: ADC and DAC
- 4: DSP Software
- 5: Linear Systems
- 6: Convolution
- 7: Properties of Convolution
- 8: The Discrete Fourier Transform
- 9: Applications of the DFT
- 10: Fourier Transform Properties
- 11: Fourier Transform Pairs
- 12: The Fast Fourier Transform
- 13: Continuous Signal Processing
- 14: Introduction to Digital Filters
- 15: Moving Average Filters
- 16: Windowed-Sinc Filters
- 17: Custom Filters
- 18: FFT Convolution
- 19: Recursive Filters
- 20: Chebyshev Filters
- 21: Filter Comparison
- 22: Audio Processing
- 23: Image Formation & Display
- 24: Linear Image Processing
- 25: Special Imaging Techniques
- 26: Neural Networks (and more!)
- 27: Data Compression
- 28: Digital Signal Processors
- 29: Getting Started with DSPs
- 30: Complex Numbers
- 31: The Complex Fourier Transform
- 32: The Laplace Transform
- 33: The z-Transform
- 34: Explaining Benford's Law
How to order your own hardcover copy
Wouldn't you rather have a bound book instead of 640 loose pages?Your laser printer will thank you!
Order from Amazon.com.
Chapter 16: Windowed-Sinc Filters
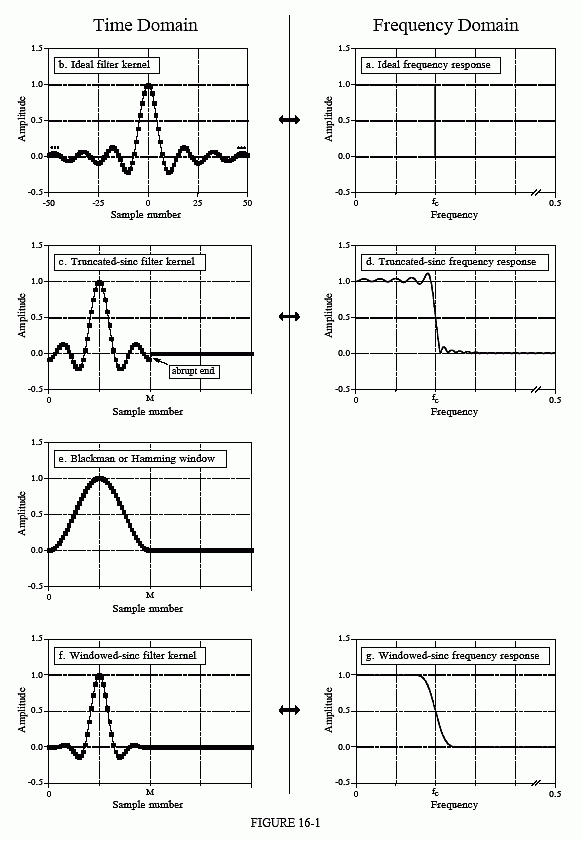
Figure 16-1 illustrates the idea behind the windowed-sinc filter. In (a), the frequency response of the ideal low-pass filter is shown. All frequencies below the cutoff frequency, fc, are passed with unity amplitude, while all higher frequencies are blocked. The passband is perfectly flat, the attenuation in the stopband is infinite, and the transition between the two is infinitesimally small.
Taking the Inverse Fourier Transform of this ideal frequency response produces the ideal filter kernel (impulse response) shown in (b). As previously discussed (see Chapter 11, Eq. 11-4), this curve is of the general form: , called the sinc function, given by:
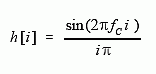
Convolving an input signal with this filter kernel provides a perfect low-pass filter. The problem is, the sinc function continues to both negative and positive infinity without dropping to zero amplitude. While this infinite length is not a problem for mathematics, it is a show stopper for computers.
To get around this problem, we will make two modifications to the sinc function in (b), resulting in the waveform shown in (c). First, it is truncated to M + 1 points, symmetrically chosen around the main lobe, where M is an even number. All samples outside these M + 1 points are set to zero, or simply ignored. Second, the entire sequence is shifted to the right so that it runs from 0 to M. This allows the filter kernel to be represented using only positive indexes. While many programming languages allow negative indexes, they are a nuisance to use. The sole effect of this M/2 shift in the filter kernel is to shift the output signal by the same amount.
Since the modified filter kernel is only an approximation to the ideal filter kernel, it will not have an ideal frequency response. To find the frequency response that is obtained, the Fourier transform can be taken of the signal in (c), resulting in the curve in (d). It's a mess! There is excessive ripple in the passband and poor attenuation in the stopband (recall the Gibbs effect discussed in Chapter 11). These problems result from the abrupt discontinuity at the ends of the truncated sinc function. Increasing the length of the filter kernel does not reduce these problems; the discontinuity is significant no matter how long M is made.
Fortunately, there is a simple method of improving this situation. Figure (e) shows a smoothly tapered curve called a Blackman window. Multiplying the truncated-sinc, (c), by the Blackman window, (e), results in the windowed-sinc filter kernel shown in (f). The idea is to reduce the abruptness of the truncated ends and thereby improve the frequency response. Figure (g) shows this improvement. The passband is now flat, and the stopband attenuation is so good it cannot be seen in this graph.
Several different windows are available, most of them named after their original developers in the 1950s. Only two are worth using, the Hamming window and the Blackman window These are given by:
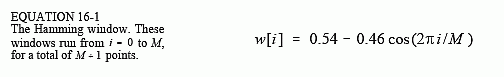
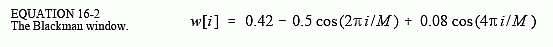
Figure 16-2a shows the shape of these two windows for (i.e., 51 total points in the curves). Which of these two windows should you use? It's a trade-off between parameters. As shown in Fig. 16-2b, the Hamming window has about a 20% faster roll-off than the Blackman. However,

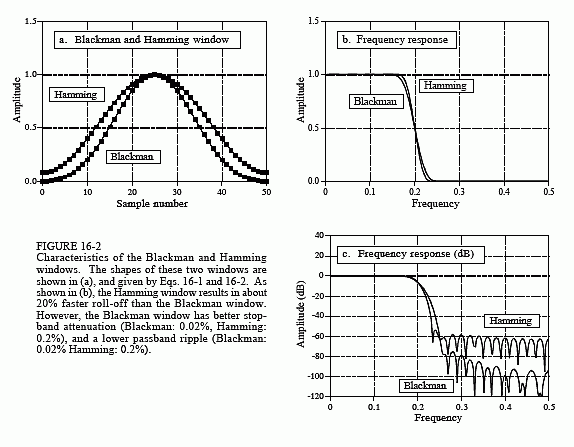
(c) shows that the Blackman has a better stopband attenuation. To be exact, the stopband attenuation for the Blackman is -74dB (∼0.02%), while the Hamming is only -53dB (∼0.2%). Although it cannot be seen in these graphs, the Blackman has a passband ripple of only about 0.02%, while the Hamming is typically 0.2%. In general, the Blackman should be your first choice; a slow roll-off is easier to handle than poor stopband attenuation.
There are other windows you might hear about, although they fall short of the Blackman and Hamming. The Bartlett window is a triangle, using straight lines for the taper. The Hanning window, also called the raised cosine window, is given by: . These two windows have about the same roll-off speed as the Hamming, but worse stopband attenuation (Bartlett: -25dB or 5.6%, Hanning -44dB or 0.63%). You might also hear of a rectangular window. This is the same as no window, just a truncation of the tails (such as in 16-1c). While the roll-off is ∼2.5 times faster than the Blackman, the stopband attenuation is only -21dB (8.9%).
