The Scientist and Engineer's Guide to
Digital Signal Processing
By Steven W. Smith, Ph.D.
Book Search
Table of contents
- 1: The Breadth and Depth of DSP
- 2: Statistics, Probability and Noise
- 3: ADC and DAC
- 4: DSP Software
- 5: Linear Systems
- 6: Convolution
- 7: Properties of Convolution
- 8: The Discrete Fourier Transform
- 9: Applications of the DFT
- 10: Fourier Transform Properties
- 11: Fourier Transform Pairs
- 12: The Fast Fourier Transform
- 13: Continuous Signal Processing
- 14: Introduction to Digital Filters
- 15: Moving Average Filters
- 16: Windowed-Sinc Filters
- 17: Custom Filters
- 18: FFT Convolution
- 19: Recursive Filters
- 20: Chebyshev Filters
- 21: Filter Comparison
- 22: Audio Processing
- 23: Image Formation & Display
- 24: Linear Image Processing
- 25: Special Imaging Techniques
- 26: Neural Networks (and more!)
- 27: Data Compression
- 28: Digital Signal Processors
- 29: Getting Started with DSPs
- 30: Complex Numbers
- 31: The Complex Fourier Transform
- 32: The Laplace Transform
- 33: The z-Transform
- 34: Explaining Benford's Law
How to order your own hardcover copy
Wouldn't you rather have a bound book instead of 640 loose pages?Your laser printer will thank you!
Order from Amazon.com.
Chapter 12: The Fast Fourier Transform
When the DFT is calculated by correlation (as in Table 12-2), the program uses two nested loops, each running through N points. This means that the total number of operations is proportional to N times N. The time to complete the program is thus given by:
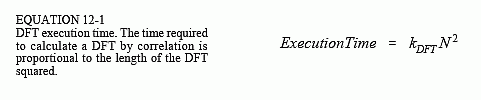
where N is the number of points in the DFT and kDFT is a constant of proportionality. If the sine and cosine values are calculated within the nested loops, kDFT is equal to about 25 microseconds on a Pentium at 100 MHz. If you precalculate the sine and cosine values and store them in a look-up-table, kDFT drops to about 7 microseconds. For example, a 1024 point DFT will require about 25 seconds, or nearly 25 milliseconds per point. That's slow!
Using this same strategy we can derive the execution time for the FFT. The time required for the bit reversal is negligible. In each of the Log2N stages there are N/2 butterfly computations. This means the execution time for the program is approximated by:
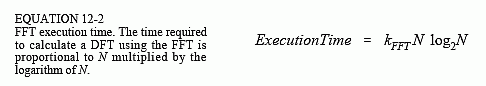
The value of kFFT is about 10 microseconds on a 100 MHz Pentium system. A 1024 point FFT requires about 70 milliseconds to execute, or 70 microseconds per point. This is more than 300 times faster than the DFT calculated by correlation!
Not only is NLog2N less than N2, it increases much more slowly as N becomes larger. For example, a 32 point FFT is about ten times faster than the correlation method. However, a 4096 point FFT is one-thousand times faster. For small values of N (say, 32 to 128), the FFT is important. For large values of N (1024 and above), the FFT is absolutely critical. Figure 12-8 compares the execution times of the two algorithms in a graphical form.
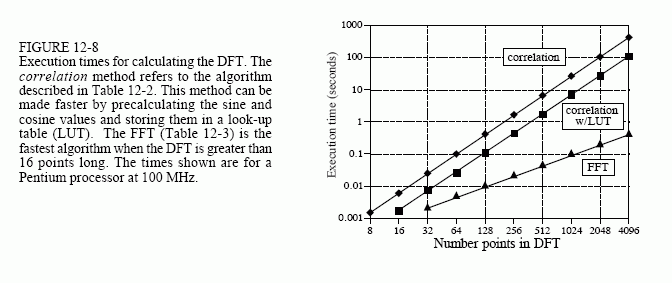
The FFT has another advantage besides raw speed. The FFT is calculated more precisely because the fewer number of calculations results in less round-off error. This can be demonstrated by taking the FFT of an arbitrary signal, and then running the frequency spectrum through an Inverse FFT. This reconstructs the original time domain signal, except for the addition of round-off noise from the calculations. A single number characterizing this noise can be obtained by calculating the standard deviation of the difference between the two signals. For comparison, this same procedure can be repeated using a DFT calculated by correlation, and a corresponding Inverse DFT. How does the round-off noise of the FFT compare to the DFT by correlation? See for yourself in Fig. 12-9.
