The Scientist and Engineer's Guide to
Digital Signal Processing
By Steven W. Smith, Ph.D.
Book Search
Table of contents
- 1: The Breadth and Depth of DSP
- 2: Statistics, Probability and Noise
- 3: ADC and DAC
- 4: DSP Software
- 5: Linear Systems
- 6: Convolution
- 7: Properties of Convolution
- 8: The Discrete Fourier Transform
- 9: Applications of the DFT
- 10: Fourier Transform Properties
- 11: Fourier Transform Pairs
- 12: The Fast Fourier Transform
- 13: Continuous Signal Processing
- 14: Introduction to Digital Filters
- 15: Moving Average Filters
- 16: Windowed-Sinc Filters
- 17: Custom Filters
- 18: FFT Convolution
- 19: Recursive Filters
- 20: Chebyshev Filters
- 21: Filter Comparison
- 22: Audio Processing
- 23: Image Formation & Display
- 24: Linear Image Processing
- 25: Special Imaging Techniques
- 26: Neural Networks (and more!)
- 27: Data Compression
- 28: Digital Signal Processors
- 29: Getting Started with DSPs
- 30: Complex Numbers
- 31: The Complex Fourier Transform
- 32: The Laplace Transform
- 33: The z-Transform
- 34: Explaining Benford's Law
How to order your own hardcover copy
Wouldn't you rather have a bound book instead of 640 loose pages?Your laser printer will thank you!
Order from Amazon.com.
Chapter 4: DSP Software
While computer hardware and programming languages are important for maximizing execution speed, they are not something you change on a day-to day basis. In comparison, how you program can be changed at any time, and will drastically affect how long the program will require to execute. Here are three suggestions.
First, use integers instead of floating point variables whenever possible. Conventional microprocessors, such as used in personal computers, process integers 10 to 20 times faster than floating point numbers. On systems without a math coprocessor, the difference can be 200 to 1. An exception to this is integer division, which is often accomplished by converting the values into floating point. This makes the operation ghastly slow compared to other integer calculations. See Table 4-6 for details.
Second, avoid using functions such as: , etc. These transcendental functions are calculated as a series of additions, subtractions and multiplications. For example, the Maclaurin power series provides:
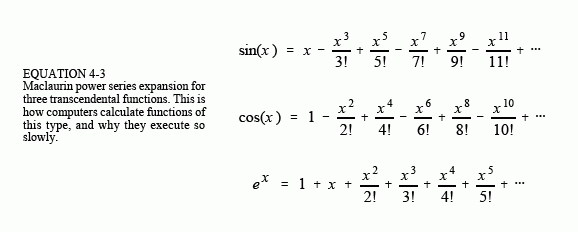
While these relations are infinite in length, the terms rapidly become small enough to be ignored. For example:
These functions require about ten times longer to calculate than a single addition or multiplication (see Table 4-6). Several tricks can be used to bypass these calculations, such as: x3 = x·x·x; sin(x)≈x, when x is very small; sin(-x) = -sin(x), where you already know one of the values and need to find the other, etc. Most languages only provide a few transcendental functions, and expect you to derive the others by means of the relations in Table 4-7. Not surprisingly, these derived calculations are even slower.

Another option is to precalculate these slow functions, and store the values in a look-up table (LUT). For example, imagine an 8 bit data acquisition system used to continually monitor the voltage across a resistor. If the parameter of interest is the power being dissipated in the resistor, the measured voltage can be used to calculate: P=V2/R. As a faster alternative, the power corresponding to each of the possible 256 voltage measurements can be calculated beforehand, and stored in a LUT. When the system is running, the measured voltage, a digital number between 0 and 255, becomes an index in the LUT to find the corresponding power. Look-up tables can be hundreds of times faster than direct calculation.
Third, learn what is fast and what is slow on your particular system. This comes with experience and testing, and there will always be surprises. Pay particular attention to graphics commands and I/O. There are usually several ways to handle these requirements, and the speeds can be tremendously different. For example, the BASIC command: BLOAD, transfers a data file directly into a section of memory. Reading the same file into memory byte-by-byte (in a loop) can be 100 times as slow. As another example, the BASIC command: LINE, can be used to draw a colored box on the video screen. Drawing the same box pixel-by-pixel can also take 100 times as long. Even putting a print statement within a loop (to keep track of what it is doing) can slow the operation by thousands!
