The Scientist and Engineer's Guide to
Digital Signal Processing
By Steven W. Smith, Ph.D.
Book Search
Table of contents
- 1: The Breadth and Depth of DSP
- 2: Statistics, Probability and Noise
- 3: ADC and DAC
- 4: DSP Software
- 5: Linear Systems
- 6: Convolution
- 7: Properties of Convolution
- 8: The Discrete Fourier Transform
- 9: Applications of the DFT
- 10: Fourier Transform Properties
- 11: Fourier Transform Pairs
- 12: The Fast Fourier Transform
- 13: Continuous Signal Processing
- 14: Introduction to Digital Filters
- 15: Moving Average Filters
- 16: Windowed-Sinc Filters
- 17: Custom Filters
- 18: FFT Convolution
- 19: Recursive Filters
- 20: Chebyshev Filters
- 21: Filter Comparison
- 22: Audio Processing
- 23: Image Formation & Display
- 24: Linear Image Processing
- 25: Special Imaging Techniques
- 26: Neural Networks (and more!)
- 27: Data Compression
- 28: Digital Signal Processors
- 29: Getting Started with DSPs
- 30: Complex Numbers
- 31: The Complex Fourier Transform
- 32: The Laplace Transform
- 33: The z-Transform
- 34: Explaining Benford's Law
How to order your own hardcover copy
Wouldn't you rather have a bound book instead of 640 loose pages?Your laser printer will thank you!
Order from Amazon.com.
Chapter 26: Neural Networks (and more!)
Neural network design can best be explained with an example. Figure 26-8 shows the problem we will attack, identifying individual letters in an image of text. This pattern recognition task has received much attention. It is easy enough that many approaches achieve partial success, but difficult enough that there are no perfect solutions. Many successful commercial products have been based on this problem, such as: reading the addresses on letters for postal routing, document entry into word processors, etc.
The first step in developing a neural network is to create a database of examples. For the text recognition problem, this is accomplished by printing the 26 capital letters: A,B,C,D … Y,Z, 50 times on a sheet of paper. Next, these 1300 letters are converted into a digital image by using one of the many scanning devices available for personal computers. This large digital image is then divided into small images of 10×10 pixels, each containing a single letter. This information is stored as a 1.3 Megabyte database: 1300 images; 100 pixels per image; 8 bits per pixel. We will use the first 260 images in this database to train the neural network (i.e., determine the weights), and the remainder to test its performance. The database must also contain a way of identifying the letter contained in each image. For instance, an additional byte could be added to each 10×10 image, containing the letter's ASCII code. In another scheme, the position

of each 10×10 image in the database could indicate what the letter is. For example, images 0 to 49 might all be an "A", images 50-99 might all be a "B", etc.
For this demonstration, the neural network will be designed for an arbitrary task: determine which of the 10×10 images contains a vowel, i.e., A, E, I, O, or U. This may not have any practical application, but it does illustrate the ability of the neural network to learn very abstract pattern recognition problems. By including ten examples of each letter in the training set, the network will (hopefully) learn the key features that distinguish the target from the nontarget images.
The neural network used in this example is the traditional three-layer, fully interconnected architecture, as shown in Figs. 26-5 and 26-6. There are 101 nodes in the input layer (100 pixel values plus a bias node), 10 nodes in the hidden layer, and 1 node in the output layer. When a 100 pixel image is applied to the input of the network, we want the output value to be close to one if a vowel is present, and near zero if a vowel is not present. Don't be worried that the input signal was acquired as a two-dimensional array (10×10), while the input to the neural network is a one-dimensional array. This is your understanding of how the pixel values are interrelated; the neural network will find relationships of its own.
Table 26-2 shows the main program for calculating the neural network weights, with Table 26-3 containing three subroutines called from the main program. The array elements: X1[1] through X1[100], hold the input layer values. In addition, X1[101] always holds a value of 1, providing the input to the bias node. The output values from the hidden nodes are contained

in the array elements: X2[1] through X2[10]. The variable, X3, contains the network's output value. The weights of the hidden layer are contained in the array, WH[ , ], where the first index identifies the hidden node (1 to 10), and the second index is the input layer node (1 to 101). The weights of the output layer are held in WO[1] to WO[10]. This makes a total of 1020 weight values that define how the network will operate.
The first action of the program is to set each weight to an arbitrary initial value by using a random number generator. As shown in lines 190 to 240, the hidden layer weights are assigned initial values between -0.0005 and 0.0005, while the output layer weights are between -0.5 and 0.5. These ranges are chosen to be the same order of magnitude that the final weights must be. This is based on: (1) the range of values in the input signal, (2) the number of inputs summed at each node, and (3) the range of values over which the sigmoid is active, an input of about -5 < x < 5, and an output of 0 to 1. For instance, when 101 inputs with a typical value of 100 are multiplied by the typical weight value of 0.0002, the sum of the products is about 2, which is in the active range of the sigmoid's input.
If we evaluated the performance of the neural network using these random weights, we would expect it to be the same as random guessing. The learning algorithm improves the performance of the network by gradually changing each weight in the proper direction. This is called an iterative procedure, and is controlled in the program by the FOR-NEXT loop in lines 270-400. Each iteration makes the weights slightly more efficient at separating the target from the nontarget examples. The iteration loop is usually carried out until no further improvement is being made. In typical neural networks, this may be anywhere from ten to ten-thousand iterations, but a few hundred is common. This example carries out 800 iterations.
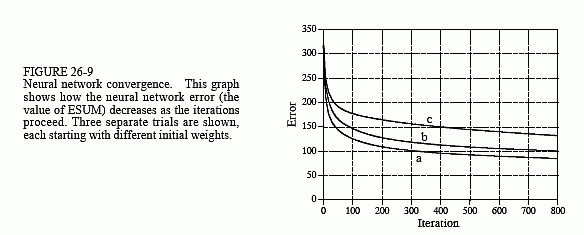
In order for this iterative strategy to work, there must be a single parameter that describes how well the system is currently performing. The variable ESUM (for error sum) serves this function in the program. The first action inside the iteration loop is to set ESUM to zero (line 290) so that it can be used as an accumulator. At the end of each iteration, the value of ESUM is printed to the video screen (line 380), so that the operator can insure that progress is being made. The value of ESUM will start high, and gradually decrease as the neural network is trained to recognize the targets. Figure 26-9 shows examples of how ESUM decreases as the iterations proceed.
All 260 images in the training set are evaluated during each iteration, as controlled by the FOR-NEXT loop in lines 310-360. Subroutine 1000 is used to retrieve images from the database of examples. Since this is not something of particular interest here, we will only describe the parameters passed to and from this subroutine. Subroutine 1000 is entered with the parameter, LETTER%, being between 1 and 260. Upon return, the input node values, X1[1] to X1[100], contain the pixel values for the image in the database corresponding to LETTER%. The bias node value, X1[101], is always returned with a constant value of one. Subroutine 1000 also returns another parameter, CORRECT. This contains the desired output value of the network for this particular letter. That is, if the letter in the image is a vowel, CORRECT will be returned with a value of one. If the letter in the image is not a vowel, CORRECT will be returned with a value of zero.
After the image being worked on is loaded into X1[1] through X1[100], subroutine 2000 passes the data through the current neural network to produce the output node value, X3. In other words, subroutine 2000 is the same as the program in Table 26-1, except for a different number of nodes in each layer. This subroutine also calculates how well the current network identifies the letter as a target or a nontarget. In line 2210, the variable ELET (for error-letter) is calculated as the difference between the output value actually generated, X3, and the desired value, CORRECT. This makes ELET a value between -1 and 1. All of the 260 values for ELET are combined (line 340) to form ESUM, the total squared error of the network for the entire training set.
Line 2220 shows an option that is often included when calculating the error: assigning a different importance to the errors for targets and nontargets. For example, recall the cancer example presented earlier in this chapter,

and the consequences of making a false-positive error versus a false-negative error. In the present example, we will arbitrarily declare that the error in detecting a target is five times as bad as the error in detecting a nontarget. In effect, this tells the network to do a better job with the targets, even if it hurts the performance of the nontargets.
Subroutine 3000 is the heart of the neural network strategy, the algorithm for changing the weights on each iteration. We will use an analogy to explain the underlying mathematics. Consider the predicament of a military paratrooper dropped behind enemy lines. He parachutes to the ground in unfamiliar territory, only to find it is so dark he can't see more than a few feet away. His orders are to proceed to the bottom of the nearest valley to begin the remainder of his mission. The problem is, without being able to see more than a few feet, how does he make his way to the valley floor? Put another way, he needs an algorithm to adjust his x and y position on the earth's surface in order to minimize his elevation. This is analogous to the problem of adjusting the neural network weights, such that the network's error, ESUM, is minimized.
We will look at two algorithms to solve this problem: evolution and steepest descent. In evolution, the paratrooper takes a flying jump in some random direction. If the new elevation is higher than the previous, he curses and returns to his starting location, where he tries again. If the new elevation is lower, he feels a measure of success, and repeats the process from the new location. Eventually he will reach the bottom of the valley, although in a very inefficient and haphazard path. This method is called evolution because it is the same type of algorithm employed by nature in biological evolution. Each new generation of a species has random variations from the previous. If these differences are of benefit to the species, they are more likely to be retained and passed to the next generation. This is a result of the improvement allowing the animal to receive more food, escape its enemies, produce more offspring, etc. If the new trait is detrimental, the disadvantaged animal becomes lunch for some predator, and the variation is discarded. In this sense, each new generation is an iteration of the evolutionary optimization procedure.
When evolution is used as the training algorithm, each weight in the neural network is slightly changed by adding the value from a random number generator. If the modified weights make a better network (i.e., a lower value for ESUM), the changes are retained, otherwise they are discarded. While this works, it is very slow in converging. This is the jargon used to describe that continual improvement is being made toward an optimal solution (the bottom of the valley). In simpler terms, the program is going to need days to reach a solution, rather than minutes or hours.
Fortunately, the steepest descent algorithm is much faster. This is how the paratrooper would naturally respond: evaluate which way is downhill, and move in that direction. Think about the situation this way. The paratrooper can move one step to the north, and record the change in elevation. After returning to his original position, he can take one step to the east, and
record that elevation change. Using these two values, he can determine which direction is downhill. Suppose the paratrooper drops 10 cm when he moves one step in the northern direction, and drops 20 cm when he moves one step in the eastern direction. To travel directly downhill, he needs to move along each axis an amount proportional to the slope along that axis. In this case, he might move north by 10 steps and east by 20 steps. This moves him down the steepest part of the slope a distance of √102 + 202 steps. Alternatively, he could move in a straight line to the new location, 22.4 steps along the diagonal. The key point is: the steepest descent is achieved by moving along each axis a distance proportional to the slope along that axis.
Subroutine 3000 implements this same steepest decent algorithm for the network weights. Before entering subroutine 3000, one of the example images has been applied to the input layer, and the information propagated to the output. This means that the values for: X1[ ], X2[ ] and X3 are all specified, as well as the current weight values: WH[ , ] and WO[ ]. In addition, we know the error the network produces for this particular image, ELET. The hidden layer weights are updated in lines 3050 to 3120, while the output layer weights are modified in lines 3150 to 3190. This is done by calculating the slope for each weight, and then changing each weight by an amount proportional to that slope. In the paratrooper case, the slope along an axis is found by moving a small distance along the axis (say, Δx), measuring the change in elevation (say, ΔE), and then dividing the two (ΔE/Δx). The slope of a neural network weight can be found in this same way: add a small increment to the weight value (Δw), find the resulting change in the output signal (ΔX3), and divide the two (ΔX3/Δw). Later in this chapter we will look at an example that calculates the slope this way. However, in the present example we will use a more efficient method.
Earlier we said that the nonlinearity (the sigmoid) needs to be differentiable. Here is where we will use this property. If we know the slope at each point on the nonlinearity, we can directly write an equation for the slope of each weight (ΔX3/Δw) without actually having to perturb it. Consider a specific weight, for example, WO[1], corresponding to the first input of the output node. Look at the structure in Figs. 26-5 and 26-6, and ask: how will the output (X3) be affected if this particular weight (w) is changed slightly, but everything else is kept the same? The answer is:

where SLOPEO is the first derivative of the output layer sigmoid, evaluated where we are operating on its curve. In other words, SLOPEO describes how much the output of the sigmoid changes in response to a change in the input to the sigmoid. From Eq. 26-2, SLOPEO can be calculated from the current output value of the sigmoid, X3. This calculation is shown in line 3160. In line 3170, the slope for this weight is calculated via Eq. 26-3, and stored in the variable DX3DW (i.e., ΔX3/Δw).
Using a similar analysis, the slope for a weight on the hidden layer, such as WH[1,1], can be found by:
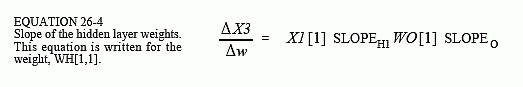
SLOPEH1 is the first derivative of the hidden layer sigmoid, evaluated where we are operating on its curve. The other values, X1[1] and WO[1], are simply constants that the weight change sees as it makes its way to the output. In lines 3070 and 3080, the slopes of the sigmoids are calculated using Eq. 26-2. The slope of the hidden layer weight, DX3DW is calculated in line 3090 via Eq. 26-4.
Now that we know the slope of each of the weights, we can look at how each weight is changed for the next iteration. The new value for each weight is found by taking the current weight, and adding an amount that is proportional to the slope:
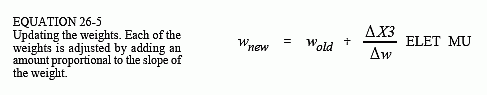
This calculation is carried out in line 3100 for the hidden layer, and line 3180 for the output layer. The proportionality constant consists of two factors, ELET, the error of the network for this particular input, and MU, a constant set at the beginning of the program. To understand the need for ELET in this calculation, imagine that an image placed on the input produces a small error in the output signal. Next, imagine that another image applied to the input produces a large output error. When adjusting the weights, we want to nudge the network more for the second image than the first. If something is working poorly, we want to change it; if it is working well, we want to leave it alone. This is accomplished by changing each weight in proportion to the current error, ELET.
To understand how MU affects the system, recall the example of the paratrooper. Once he determines the downhill direction, he must decide how far to proceed before reevaluating the slope of the terrain. By making this distance short, one meter for example, he will be able to precisely follow the contours of the terrain and always be moving in an optimal direction. The problem is that he spends most of his time evaluating the slope, rather than actually moving down the hill. In comparison, he could choose the distance to be large, say 1000 meters. While this would allow the paratrooper to move rapidly along the terrain, he might overshoot the downhill path. Too large of a distance makes him jump all over the country-side without making the desired progress.
In the neural network, MU controls how much the weights are changed on each iteration. The value to use depends on the particular problem, being as low as 10-6, or as high as 0.1. From the analogy of the paratrooper, it can be expected that too small of a value will cause the network to converge too slowly. In comparison, too large of a value will cause the convergence to be erratic, and will exhibit chaotic oscillation around the final solution. Unfortunately, the way neural networks react to various values of MU can be difficult to understand or predict. This makes it critical that the network error (i.e., ESUM) be monitored during the training, such as printing it to the video screen at the end of each iteration. If the system isn't converging properly, stop the program and try another value for MU.
