The Scientist and Engineer's Guide to
Digital Signal Processing
By Steven W. Smith, Ph.D.
Book Search
Table of contents
- 1: The Breadth and Depth of DSP
- 2: Statistics, Probability and Noise
- 3: ADC and DAC
- 4: DSP Software
- 5: Linear Systems
- 6: Convolution
- 7: Properties of Convolution
- 8: The Discrete Fourier Transform
- 9: Applications of the DFT
- 10: Fourier Transform Properties
- 11: Fourier Transform Pairs
- 12: The Fast Fourier Transform
- 13: Continuous Signal Processing
- 14: Introduction to Digital Filters
- 15: Moving Average Filters
- 16: Windowed-Sinc Filters
- 17: Custom Filters
- 18: FFT Convolution
- 19: Recursive Filters
- 20: Chebyshev Filters
- 21: Filter Comparison
- 22: Audio Processing
- 23: Image Formation & Display
- 24: Linear Image Processing
- 25: Special Imaging Techniques
- 26: Neural Networks (and more!)
- 27: Data Compression
- 28: Digital Signal Processors
- 29: Getting Started with DSPs
- 30: Complex Numbers
- 31: The Complex Fourier Transform
- 32: The Laplace Transform
- 33: The z-Transform
- 34: Explaining Benford's Law
How to order your own hardcover copy
Wouldn't you rather have a bound book instead of 640 loose pages?Your laser printer will thank you!
Order from Amazon.com.
Chapter 13: Continuous Signal Processing
This brings us to the last member of the Fourier transform family: the Fourier series. The time domain signal used in the Fourier series is periodic and continuous. Figure 13-10 shows several examples of continuous waveforms that repeat themselves from negative to positive infinity. Chapter 11 showed that periodic signals have a frequency spectrum consisting of harmonics. For instance, if the time domain repeats at 1000 hertz, the frequency spectrum will contain a first harmonic at 1000 hertz, a second harmonic at 2000 hertz, a third harmonic at 3000 hertz, and so forth. The first harmonic, i.e., the frequency that the time domain repeats itself, is also called the fundamental frequency. This means that the frequency spectrum can be viewed in two ways: (1) the frequency spectrum is continuous, but zero at all frequencies except the harmonics, or (2) the frequency spectrum is discrete, and only defined at the harmonic frequencies. In other words, the frequencies between the harmonics can be thought of as having a value of zero, or simply not existing. The important point is that they do not contribute to forming the time domain signal.
The Fourier series synthesis equation creates a continuous periodic signal with a fundamental frequency, f, by adding scaled cosine and sine waves with frequencies: f, 2f, 3f, 4f, etc. The amplitudes of the cosine waves are held in the variables: a1, a2, a3, a3, etc., while the amplitudes of the sine waves are held in: b1, b2, b3, b4, and so on. In other words, the "a" and "b" coefficients are the real and imaginary parts of the frequency spectrum, respectively. In addition, the coefficient a0 is used to hold the DC value of the time domain waveform. This can be viewed as the amplitude of a cosine wave with zero frequency (a constant value). Sometimes is grouped with the other "a" coefficients, but it is often handled separately because it requires special calculations. There is no b0 coefficient since a sine wave of zero frequency has a constant value of zero, and would be quite useless. The synthesis equation is written:
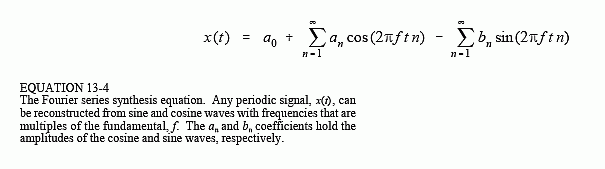
The corresponding analysis equations for the Fourier series are usually written in terms of the period of the waveform, denoted by T, rather than the fundamental frequency, f (where f = 1/T). Since the time domain signal is periodic, the sine and cosine wave correlation only needs to be evaluated over a single period, i.e., -T/2 to T/2, 0 to T, -T to 0, etc. Selecting different limits makes the mathematics different, but the final answer is always the same. The Fourier series analysis equations are:
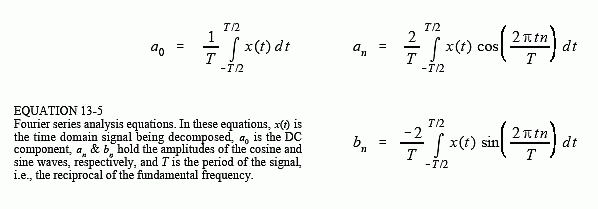
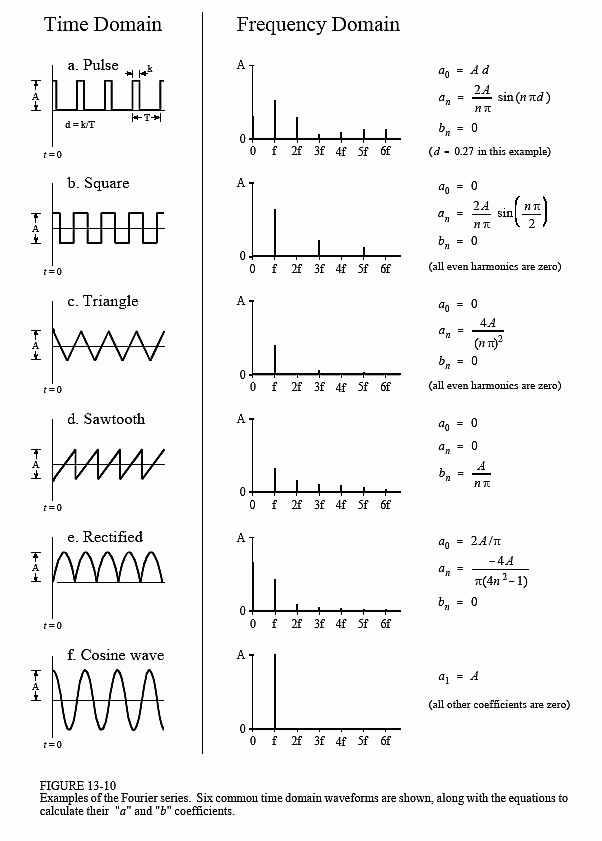
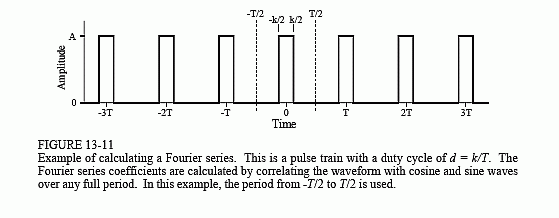
Figure 13-11 shows an example of calculating a Fourier series using these equations. The time domain signal being analyzed is a pulse train, a square wave with unequal high and low durations. Over a single period from -T/2 to T/2, the waveform is given by:
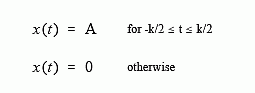
The duty cycle of the waveform (the fraction of time that the pulse is "high") is thus given by d = k/T. The Fourier series coefficients can be found by evaluating Eq. 13-5. First, we will find the DC component, a0:
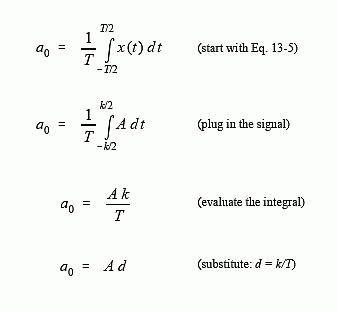
This result should make intuitive sense; the DC component is simply the average value of the signal. A similar analysis provides the "a" coefficients:
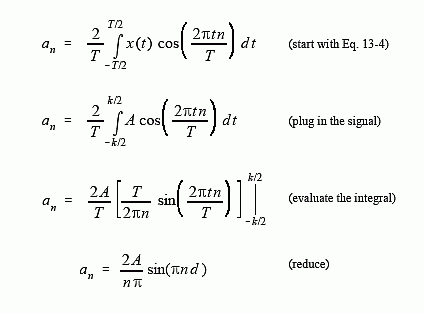
The "b" coefficients are calculated in this same way; however, they all turn out to be zero. In other words, this waveform can be constructed using only cosine waves, with no sine waves being needed.
The "a" and "b" coefficients will change if the time domain waveform is shifted left or right. For instance, the "b" coefficients in this example will be zero only if one of the pulses is centered on t = 0. Think about it this way. If the waveform is even (i.e., symmetrical around t = 0), it will be composed solely of even sinusoids, that is, cosine waves. This makes all of the "b" coefficients equal to zero. If the waveform if odd (i.e., symmetrical but opposite in sign around t = 0), it will be composed of odd sinusoids, i.e., sine waves. This results in the "a" coefficients being zero. If the coefficients are converted to polar notation (say, Mn and θn coefficients), a shift in the time domain leaves the magnitude unchanged, but adds a linear component to the phase.
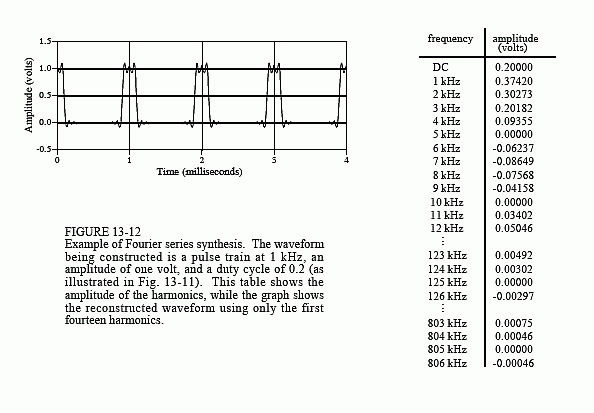
To complete this example, imagine a pulse train existing in an electronic circuit, with a frequency of 1 kHz, an amplitude of one volt, and a duty cycle of 0.2. The table in Fig. 13-12 provides the amplitude of each harmonic contained in this waveform. Figure 13-12 also shows the synthesis of the waveform using only the first fourteen of these harmonics. Even with this number of harmonics, the reconstruction is not very good. In mathematical jargon, the Fourier series converges very slowly. This is just another way of saying that sharp edges in the time domain waveform results in very high frequencies in the spectrum. Lastly, be sure and notice the overshoot at the sharp edges, i.e., the Gibbs effect discussed in Chapter 11.
An important application of the Fourier series is electronic frequency multiplication. Suppose you want to construct a very stable sine wave oscillator at 150 MHz. This might be needed, for example, in a radio transmitter operating at this frequency. High stability calls for the circuit to be crystal controlled. That is, the frequency of the oscillator is determined by a resonating quartz crystal that is a part of the circuit. The problem is, quartz crystals only work to about 10 MHz. The solution is to build a crystal controlled oscillator operating somewhere between 1 and 10 MHz, and then multiply the frequency to whatever you need. This is accomplished by distorting the sine wave, such as by clipping the peaks with a diode, or running the waveform through a squaring circuit. The harmonics in the distorted waveform are then isolated with band-pass filters. This allows the frequency to be doubled, tripled, or multiplied by even higher integers numbers. The most common technique is to use sequential stages of doublers and triplers to generate the required frequency multiplication, rather than just a single stage. The Fourier series is important to this type of design because it describes the amplitude of the multiplied signal, depending on the type of distortion and harmonic selected.