The Scientist and Engineer's Guide to
Digital Signal Processing
By Steven W. Smith, Ph.D.
Book Search
Table of contents
- 1: The Breadth and Depth of DSP
- 2: Statistics, Probability and Noise
- 3: ADC and DAC
- 4: DSP Software
- 5: Linear Systems
- 6: Convolution
- 7: Properties of Convolution
- 8: The Discrete Fourier Transform
- 9: Applications of the DFT
- 10: Fourier Transform Properties
- 11: Fourier Transform Pairs
- 12: The Fast Fourier Transform
- 13: Continuous Signal Processing
- 14: Introduction to Digital Filters
- 15: Moving Average Filters
- 16: Windowed-Sinc Filters
- 17: Custom Filters
- 18: FFT Convolution
- 19: Recursive Filters
- 20: Chebyshev Filters
- 21: Filter Comparison
- 22: Audio Processing
- 23: Image Formation & Display
- 24: Linear Image Processing
- 25: Special Imaging Techniques
- 26: Neural Networks (and more!)
- 27: Data Compression
- 28: Digital Signal Processors
- 29: Getting Started with DSPs
- 30: Complex Numbers
- 31: The Complex Fourier Transform
- 32: The Laplace Transform
- 33: The z-Transform
- 34: Explaining Benford's Law
How to order your own hardcover copy
Wouldn't you rather have a bound book instead of 640 loose pages?Your laser printer will thank you!
Order from Amazon.com.
Chapter 21: Filter Comparison
Most digital signals originate in analog electronics. If the signal needs to be filtered, is it better to use an analog filter before digitization, or a digital filter after? We will answer this question by letting two of the best contenders deliver their blows.
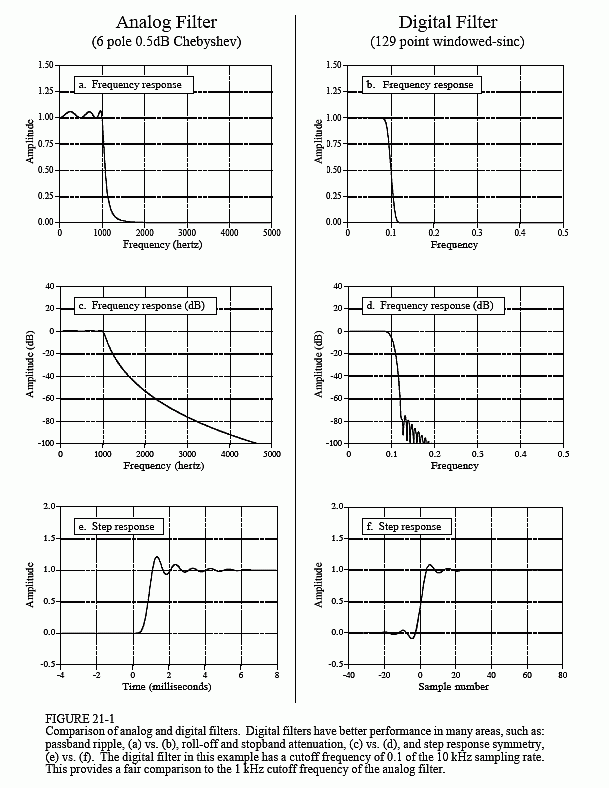
The goal will be to provide a low-pass filter at 1 kHz. Fighting for the analog side is a six pole Chebyshev filter with 0.5 dB (6%) ripple. As described in Chapter 3, this can be constructed with 3 op amps, 12 resistors, and 6 capacitors. In the digital corner, the windowed-sinc is warming up and ready to fight. The analog signal is digitized at a 10 kHz sampling rate, making the cutoff frequency 0.1 on the digital frequency scale. The length of the windowed-sinc will be chosen to be 129 points, providing the same 90% to 10% roll-off as the analog filter. Fair is fair. Figure 21-1 shows the frequency and step responses for these two filters.
Let's compare the two filters blow-by-blow. As shown in (a) and (b), the analog filter has a 6% ripple in the passband, while the digital filter is perfectly flat (within 0.02%). The analog designer might argue that the ripple can be selected in the design; however, this misses the point. The flatness achievable with analog filters is limited by the accuracy of their resistors and capacitors. Even if a Butterworth response is designed (i.e., 0% ripple), filters of this complexity will have a residue ripple of, perhaps, 1%. On the other hand, the flatness of digital filters is primarily limited by round-off error, making them hundreds of times flatter than their analog counterparts. Score one point for the digital filter.
Next, look at the frequency response on a log scale, as shown in (c) and (d). Again, the digital filter is clearly the victor in both roll-off and stopband attenuation. Even if the analog performance is improved by adding additional stages, it still can't compare to the digital filter. For instance, imagine that you need to improve these two parameters by a factor of 100. This can be done with simple modifications to the windowed-sinc, but is virtually impossible for the analog circuit. Score two more for the digital filter.
The step response of the two filters is shown in (e) and (f). The digital filter's step response is symmetrical between the lower and upper portions of the step, i.e., it has a linear phase. The analog filter's step response is not symmetrical, i.e., it has a nonlinear phase. One more point for the digital filter. Lastly, the analog filter overshoots about 20% on one side of the step. The digital filter overshoots about 10%, but on both sides of the step. Since both are bad, no points are awarded.
In spite of this beating, there are still many applications where analog filters should, or must, be used. This is not related to the actual performance of the filter (i.e., what goes in and what comes out), but to the general advantages that analog circuits have over digital techniques. The first advantage is speed: digital is slow; analog is fast. For example, a personal computer can only filter data at about 10,000 samples per second, using FFT convolution. Even simple op amps can operate at 100 kHz to 1 MHz, 10 to 100 times as fast as the digital system!
The second inherent advantage of analog over digital is dynamic range. This comes in two flavors. Amplitude dynamic range is the ratio between the largest signal that can be passed through a system, and the inherent noise of the system. For instance, a 12 bit ADC has a saturation level of 4095, and an rms quantization noise of 0.29 digital numbers, for a dynamic range of about 14000. In comparison, a standard op amp has a saturation voltage of about 20 volts and an internal noise of about 2 microvolts, for a dynamic range of about ten million. Just as before, a simple op amp devastates the digital system.
The other flavor is frequency dynamic range. For example, it is easy to design an op amp circuit to simultaneously handle frequencies between 0.01 Hz and 100 kHz (seven decades). When this is tried with a digital system, the computer becomes swamped with data. For instance, sampling at 200 kHz, it takes 20 million points to capture one complete cycle at 0.01 Hz. You may have noticed that the frequency response of digital filters is almost always plotted on a linear frequency scale, while analog filters are usually displayed with a logarithmic frequency. This is because digital filters need
a linear scale to show their exceptional filter performance, while analog filters need the logarithmic scale to show their huge dynamic range.
