The Scientist and Engineer's Guide to
Digital Signal Processing
By Steven W. Smith, Ph.D.

• Home
• The Book by Chapters
• About the Book
  • Copyright and permissible use
  • What is DSP?
  • 8 good reasons for learning DSP
  • Comments by reviewers
  • Errata
  • Free Software and Teaching Aids
  • Differences Between Editions
• Steven W. Smith
• Blog
• Contact

Since the time and frequency domains are equivalent representations of the same signal, they must have the same energy. This is called Parseval's relation, and holds for all members of the Fourier transform family. For the DFT, Parseval's relation is expressed:

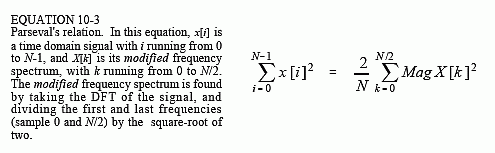
The left side of this equation is the total energy contained in the time domain signal, found by summing the energies of the N individual samples.

Likewise, the right side is the energy contained in the frequency domain, found by summing the energies of the N/2 + 1 sinusoids. Remember from physics that energy is proportional to the amplitude squared. For example, the energy in a spring is proportional to the displacement squared, and the energy stored in a capacitor is proportional to the voltage squared. In Eq. 10-1, X[f] is the frequency spectrum of x[n], with one slight modification: the first and last frequency components, X[0] & X[N/2], have been divided by √2. This modification, along with the 2/N factor on the right side of the equation, accounts for several subtle details of calculating and summing energies.

To understand these corrections, start by finding the frequency domain of the signal by using the DFT. Next, convert the frequency domain into the amplitudes of the sinusoids needed to reconstruct the signal, as previously defined in Eq. 8-3. This is done by dividing the first and last points (sample 0 and N/2) by 2, and then dividing all of the points by N/2. While this provides the amplitudes of the sinusoids, they are expressed as a peak amplitude, not the root-mean-square (rms) amplitude needed for energy calculations. In a sinusoid, the peak amplitude is converted to rms by dividing by √2. This correction must be made to all of the frequency domain values, except sample 0 and N/2. This is because these two sinusoids are unique; one is a constant value, while the other alternates between two constant values. For these two special cases, the peak amplitude is already equal to the rms value. All of the values in the frequency domain are squared and then summed. The last step is to divide the summed value by N, to account for each sample in the frequency domain being converted into a sinusoid that covers N values in the time domain. Working through all of these details produces Eq. 10-1.

While Parseval's relation is interesting from the physics it describes (conservation of energy), it has few practical uses in DSP.